
5.解(I)①当a=0时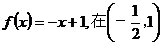 上
上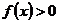 一定成立
一定成立
②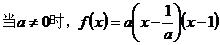

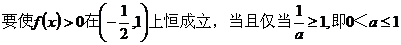 ;
;

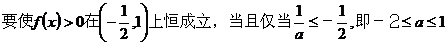
综合可得实数a的取值范围是: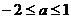 。
。
(II)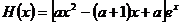 ,
,
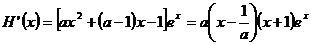
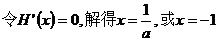
①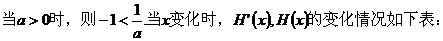
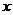 |
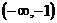 |
-1 |
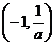 |
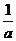 |
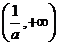 |
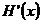 |
+ |
0 |
- |
0 |
+ |
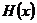 |
|
极大值 |
|
极小值 |
|
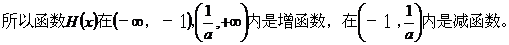

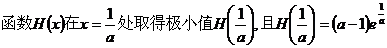
②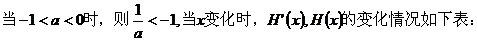
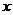 |
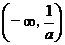 |
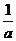 |
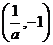 |
-1 |
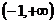 |
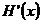 |
- |
0 |
+ |
0 |
- |
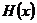 |
|
极小值 |
|
极大值 |
|
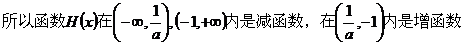

4.解设BD与AC交于O,则BD⊥AC,连结A1O,在△AA1O中,AA1=2,AO=1,∠A1AO=60O,
所以A1O2=AA12+AO2-2AA1·AOcos60O=3,
所以AO2+A1O2=AA12,所以A1O⊥AO。
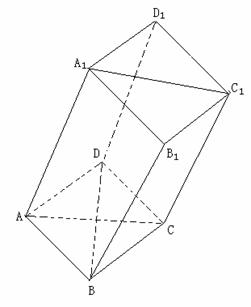
由于平面AA1C1C⊥平面ABCD,所以A1O⊥平面ABCD。
以OB,OC,OA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则
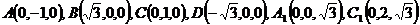
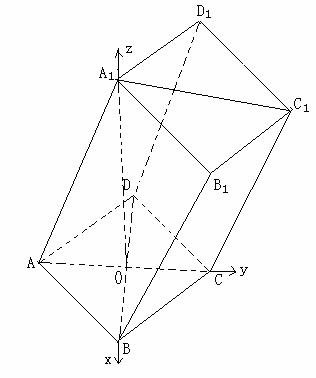
(I)由于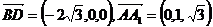 ,
,
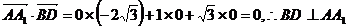
(II)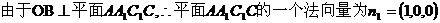

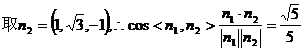
所以,二面角D-A1A-C的平面角的余弦值为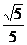
(III)假设在直线CC1上存在点P,使BP∥平面DA1C1,
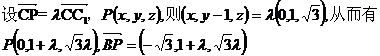
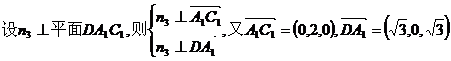
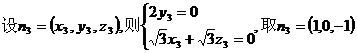
因为BP∥平面DA1C1,则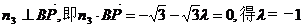
即点P在C1C的延长线上,且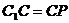
3.解:(Ⅰ)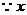 、
、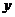 可能的取值为
可能的取值为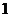 、
、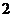 、
、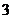 ,
,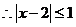 ,
,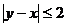 ,
,
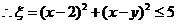 ,且当
,且当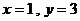 或
或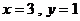 时,
时,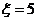 . 因此,随机变量
. 因此,随机变量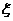 的最大值为
的最大值为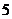 …………………………4分
…………………………4分
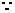 有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有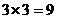 种,
种,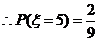 6分
6分
(Ⅱ)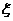 的所有取值为
的所有取值为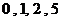 .
.
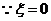 时,只有
时,只有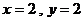 这一种情况.
这一种情况.
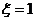 时,有
时,有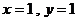 或
或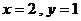 或
或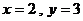 或
或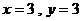 四种情况,
四种情况,
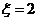 时,有
时,有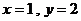 或
或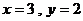 两种情况.
两种情况.
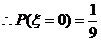 ,
,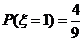 ,
,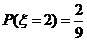 …………………………8分
…………………………8分
则随机变量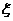 的分布列为:
的分布列为:
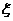
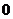
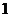
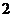
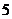
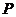
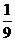
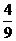
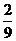
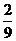
………………10分
因此,数学期望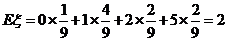 ……………12分
……………12分
2.解(I)证明:由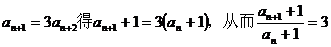
即数列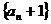 是首项为3,公比为3的等比数列
是首项为3,公比为3的等比数列
(II)由(I)知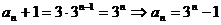 。
。
6.已知A、B是圆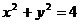 上满足条件
上满足条件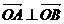 的两个点,其中O是坐标原点,分别过A、B作x轴的垂线段,交椭圆
的两个点,其中O是坐标原点,分别过A、B作x轴的垂线段,交椭圆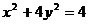 于A1、B1点,动点P满足
于A1、B1点,动点P满足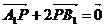
(I)求动点P的轨迹方程
(II)设S1和S2分别表示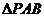 和
和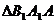 的面积,当点P在x轴的上方,点A在x轴的下方时,求S1+S2的最大值。
的面积,当点P在x轴的上方,点A在x轴的下方时,求S1+S2的最大值。
华侨中学2010届高三解答题限时训练7答案
1解:(1)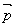 与
与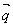 共线,有
共线,有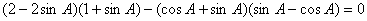 ,即
,即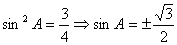 ……………………………………………………………4分
……………………………………………………………4分
因为△ABC是锐角三角形,所以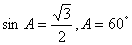 ………………………………6分
………………………………6分
(2)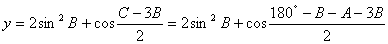
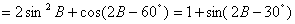 ……………………………………10分
……………………………………10分
当B=60°时,y取最大值2; 而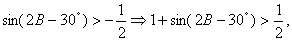
因此函数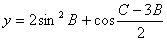 的值域为
的值域为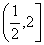 .……………………………12分
.……………………………12分
5.(本小题满分14分)
已知函数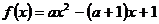
(I)当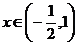 时,不等式
时,不等式 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(II)设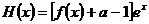 ,当
,当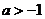 且
且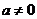 时,时求函数
时,时求函数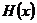 的单调区间和级值。
的单调区间和级值。
4.(本小题满分14分)
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,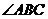 和
和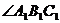 均为
均为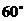 ,
,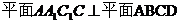 。
。
(I)求证:
(II)求二面角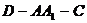 的余弦值;
的余弦值;
(III)在直线CC1上是否存在点P,使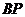 ∥平面DA1C1,若存在,求出点P的位置,若不存在,请说明理由。
∥平面DA1C1,若存在,求出点P的位置,若不存在,请说明理由。
3.(本小题满分14分)
在一个盒子中,放有标号分别为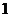 ,
,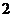 ,
,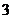 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为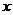 、
、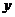 ,设
,设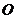 为坐标原点,点
为坐标原点,点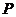 的坐标为
的坐标为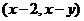 ,记
,记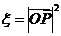 .(Ⅰ)求随机变量
.(Ⅰ)求随机变量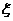 的最大值,并求事件“
的最大值,并求事件“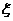 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量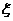 的分布列和数学期望.
的分布列和数学期望.
2.(本小题满分12分)
已知数列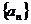 满足
满足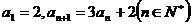
(I)求证:数列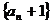 是等比数列;
是等比数列;
(II)求数列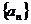 的通项公式。
的通项公式。
1.若锐角△ABC的三个内角为A、B、C,两向量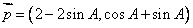 ,
,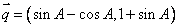 ,且
,且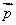 与
与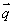 是共线向量.
是共线向量.
(1)求角A的大小; (2)求函数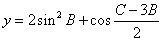 的值域
的值域
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com