
3.解法1:(Ⅰ)设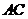 与
与 交点为
交点为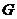 ,延长
,延长 交
交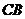 的延长线于点
的延长线于点 ,
,
则 ,∴
,∴ ,∴
,∴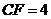 ,∴
,∴ ,
,
又∵ ,∴
,∴ ,
,
 又∵
又∵ ,∴
,∴ ,
,
∴ ,∴
,∴


 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
又∵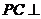 底面
底面 ,∴
,∴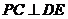 ,∴
,∴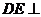 平面
平面 ,
,
∵ 平面
平面 ,∴平面
,∴平面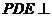 平面
平面
(Ⅱ)连结 ,过点
,过点 作
作 于
于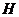 点,取
点,取 中点
中点 ,连接
,连接 ,易知
,易知
又由(Ⅰ)知平面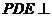 平面
平面 ,且
,且 是交线,
是交线,
根据面面垂直的性质,得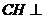 平面
平面 ,
,
由三垂线定理知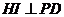 数学驿站
数学驿站
从而 为二面角
为二面角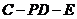 的平面角
的平面角
在等腰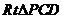 中,
中, ;
;
在 中,
中,
 ,
,
在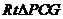 中,
中,
从而 ,则
,则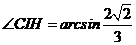
即二面角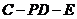 的大小为
的大小为
 (Ⅲ)由于
(Ⅲ)由于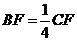 ,所以可知点
,所以可知点 到平面
到平面 的距离等于点
的距离等于点 到平面
到平面 的距离的
的距离的 ,即
,即 .
在
.
在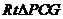 中,
中, ,
,
从而点 到平面
到平面 的距离等于
的距离等于
解法2:如图所示,以点 为坐标原点,直线
为坐标原点,直线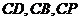 分别为
分别为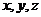 轴,
轴,
建立空间直角坐标系 ,则相关点的坐标为
,则相关点的坐标为
 ,
, ,
,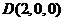 ,
, .
.

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
(Ⅰ)由于 ,
, ,
, ,
,
所以 ,
, ,
,
所以 ,
,
而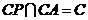 ,所以
,所以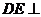 平面
平面 ,∵
,∵ 平面
平面 ,
,
∴平面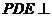 平面
平面
(Ⅱ)设 是平面
是平面 的一个法向量,则
的一个法向量,则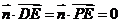 ,
由于
,
由于 ,
, ,所以有
,所以有
 ,令
,令 ,则
,则 ,即
,即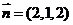 ,易知平面
,易知平面 的一个法向量
的一个法向量
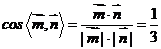 ∴二面角
∴二面角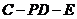 的大小为
的大小为
(Ⅲ)由(Ⅱ)知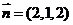 是平面
是平面 的一个法向量,而
的一个法向量,而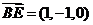 ,
,
所以点 到平面
到平面 的距离为
的距离为
2.解:(Ⅰ)记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件
 、
、 、
、 ,则
,则 ,且有
,且有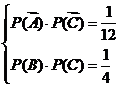 即
即
 数学驿站
数学驿站
(Ⅱ) 的可能取值:0,1,2,3
的可能取值:0,1,2,3

 |
0 |
1 |
2 |
3 |
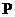 |
 |
 |
 |
 |
 .
.
6、(本小题满分14分)已知函数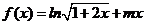 .
.
(Ⅰ)若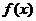 为定义域上的单调增函数,求实数
为定义域上的单调增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)当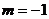 时,求函数
时,求函数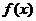 的最大值;
的最大值;
(Ⅲ)当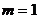 时,且
时,且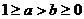 ,证明:
,证明: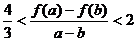 .
.
华侨中学2010届高三解答题限时训练8答案
5、(本小题满分12分)已知数列 的前n项和
的前n项和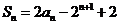
 .
.
(Ⅰ)设 ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)令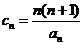 ,
, ,求证:
,求证:
 .
.
4、(本小题满分12分)设 分别是椭圆
分别是椭圆 的左、右焦点,且椭圆上一点
的左、右焦点,且椭圆上一点 到
到 两点距离之和等于4.
两点距离之和等于4.
(Ⅰ)求此椭圆方程;
(Ⅱ)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点 ,求
,求 的取值范围.
的取值范围.

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
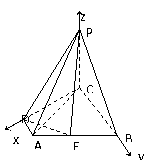
3、 (本小题满分12分)如图所示,四棱锥
(本小题满分12分)如图所示,四棱锥 的底面
的底面
为直角梯形, ,
,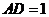 ,
, ,
,
 ,
,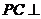 底面
底面 ,
,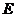 为
为 的中点.
的中点.
(Ⅰ)求证:平面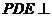 平面
平面 ;
;

 高☆考♂资♀源?网 ☆
高☆考♂资♀源?网 ☆
(Ⅱ)求二面角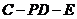 的大小;
的大小;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
2、(本小题满分12分)在某电视台举办的《上海世博会知识有奖问答比赛》中,甲、乙、丙三人同时回答一道问题,已知甲回答对这道题的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 ,且三人答对这道题的概率互不影响.
,且三人答对这道题的概率互不影响.
(Ⅰ)求乙、丙两人各自回答对这道题的概率;
(Ⅱ)求答对该题的人数 的分布列和数学期望
的分布列和数学期望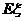 .
.
1.(本小题满分12分)
已知向量 ,
, ,设函数
,设函数 .
.
(Ⅰ)求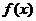 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(Ⅱ)求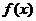 在
在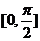 上的最小值及取得最小值时的
上的最小值及取得最小值时的 值.
值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com