
(二)有人试图利用细菌的抗病毒基因对不抗病大豆进行遗传改良,以获得抗病大豆品种。
(6)构建含外源抗病毒基因的重组DNA分子时,使用的酶有______________________。
(7)判断转基因大豆遗传改良成功的标准是__________________________________,具体的检测方法_______________________________________________________________。
(一)大豆子叶颜色(BB表现深绿;Bb表现浅绿;bb呈黄色,幼苗阶段死亡)和花叶病的抗性(由R、r基因控制)遗传的实验结果如下表:
|
组合 |
母本 |
父本 |
F1的表现型及植株数 |
|
一 |
子叶深绿不抗病 |
子叶浅绿抗病 |
子叶深绿抗病220株;子叶浅绿抗病217株 |
|
二 |
子叶深绿不抗病 |
子叶浅绿抗病 |
子叶深绿抗病110株叶深绿不抗病109株; 子叶浅绿抗病108株;子叶浅绿不抗病113株 |
(1)组合一中父本基因型是___________,组合二中父本基因型是_____________。
(2)用表中F1的子叶浅绿抗病植株自交,在F2的成熟植株中,表现型的种类有_____________
__________________________________________________,其比例为_____________。
(3)用子叶深绿与子叶浅绿植株杂交得F1,F1随机交配得到的F2成熟群体中,B基因的基因频率为________________。
(4)将表中F1的子叶浅绿抗病植株的花粉培养成单倍体植株,再将这些植株的叶肉细胞制成不同的原生质体。如要得到子叶深绿抗病植株,需要用_________________基因型的原生质体进行融合。
(5)请选用表中植物材料设计一个杂交育种方案,要求在最短的时间内选育出纯合的子叶深绿抗病大豆材料。
41(7分)基因程中经常选用的载体-pBR322质粒,Ampr表示氨苄青霉素抗性基因,Tetr表示四环素抗性基因。目的基因如果插入某抗性基因中,将使该基因失活,而不再具有相应的抗性。为了检查载体是否导入原本没有Ampr和Tetr的大肠杆菌,将大肠杆菌培养在含氨苄青霉素的培养基上,得到如图b的结果(黑点表示菌落)。再将灭菌绒布按到图b的培养基上,使绒布面沾上菌落,然后将绒布平移按到含四环素的培养基上培养,得到如图c的结果(空圈表示与b对照无菌落的位置)。据此分析并回答:
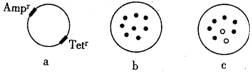
(1)pBR322质粒的基本组成单位是 。该基因工程中,质粒上的Amrr、Tetr称为 基因。
(2)与图c空圈相对应的图b中的菌落表现型是 ,由此说明目的基因
插入了 中。
(3)将大肠杆菌培养在含氨苄青霉素、四环素培养基上的过程,属于基因工程基本操作中的 步骤。该基因工程中的受体细胞是 。
(4)若用pBR322质粒作为载体,通过基因工程生产食品,是否存在食品安全性问题?试说明理由。 。
42(6分)“四位一体”(人居-种植-养殖-沼气)生态农业是我国北方典型的生态农业模式,它以沼气为纽带,将沼气池、猪禽舍、蔬菜栽培与日光温室有机地组合在一起。下图是该系统物质循环的示意图,请分析回答下列问题:
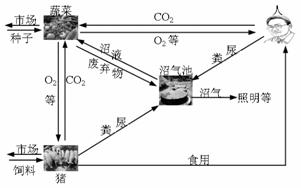
(1)人们种植的各种蔬菜在该生态系统中所属成分是 。
(2)“四位一体”主要应用了 等原理,与自然生态系统相比,它的抵抗力稳定性 (填:高、低)。
(3)当地人希望进一步提高该系统的经济效益和生态效益。专家经过考察后,建议他们增加一个奶牛养殖项目。村民接受了专家的建议,并对原有的生产项目作了一些调整。他们需要调整的项目主要是 。
(4)从图中可知,人类生活中所需的能源来自于太阳能、沼气等。利用这些能源与利用煤炭相比,它突出的优点是 。
(5)该生态工程中的能量能够更多的被人类利用,原因是
。
43(7分)生物膜系统在细胞的生命活动中起着重要的作用。请回答:
(1)细胞核的________使基因的转录和翻译两个过程在时空上分开,细胞核和细胞质之间通过________实现生物大分子的转运。
(2)脂溶性物质易透过细胞膜,表明细胞膜的主要成分中有__________通常分泌到细胞膜外的蛋白质需经过________加工和修饰后,以分泌小泡的形式排出。
(3)红细胞膜内K+浓度是膜外的30倍,膜外Na+浓度是膜内的6倍,维持这种K+,Na+分布不均匀是由膜上的________所控制;红细胞膜上糖蛋白的糖支链具有高度的特异性,若去掉这些糖支链,就不会发生红细胞的凝集反应,说明细胞膜表面这些糖蛋白是________。
(4)人工生物膜的主要用途有哪些?________(多项选择)
A.污水处理 B.食品保存 C.海水淡化处理 D.人造器官材料
44、(20分)。下面是大豆某些性状的遗传实验:
21、(本小题满分13分)
已知二次函数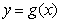 的导函数的图像与直线
的导函数的图像与直线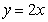 平行,且
平行,且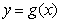 在
在 =-1处取得最小值m-1(m
=-1处取得最小值m-1(m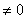 ).设函数
).设函数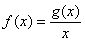
(1)若曲线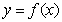 上的点P到点Q(0,2)的距离的最小值为
上的点P到点Q(0,2)的距离的最小值为 ,求m的值;
,求m的值;
(2) 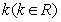 如何取值时,函数
如何取值时,函数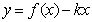 存在零点,并求出零点。
存在零点,并求出零点。
20、(本小题满分13分)
已知P、Q分别是边长为2的正三角形ABC的边AB和AC上的点.若⊿APQ的面积占⊿ABC的面积的四分之一,求PQ长的最大值与最小值.
19、(本小题满分13分)
已知函数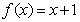 ,设
,设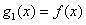 ,
,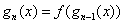
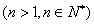
(1)求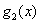 ,
,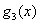 的表达式,并猜想
的表达式,并猜想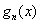
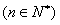 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)若关于 的函数
的函数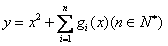 在区间
在区间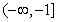 上的最小值为6,求
上的最小值为6,求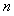 的值。(符号“
的值。(符号“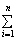 ”表示求和,例如:
”表示求和,例如: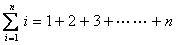 )
)
18、(本小题满分12分)
已知f(x)=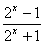 .
.
(1)判断f(x)的奇偶性;
(2)证明:方程f(x)-lnx=0至少有一根在区间(1,3)内。
17、(本小题满分12分)
设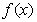 是定义在[-1,1]上的奇函数,且其图象上任意两点连线的斜率均小于零.
是定义在[-1,1]上的奇函数,且其图象上任意两点连线的斜率均小于零.
(1)证明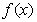 在[-1,1]上是减函数;
在[-1,1]上是减函数;
(2)如果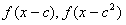 的定义域的交集为空集,求实数
的定义域的交集为空集,求实数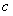 的取值范围;
的取值范围;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com