
20. 为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km,观测站B的观测半径为5km.

|
观测时刻t (分钟) |
跟踪观测点到放归点距离a(km) |
鲸位于跟踪观测点正北方向的距离b(km) |
|
10 |
1 |
1 |
|
20 |
2 |
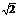 |
|
30 |
3 |
|
|
40 |
4 |
2 |
(I)根据表中数据:(1)计算鲸沿海岸线方向运动的速度,(2)写出a、b满足的关系式,并画出鲸的运动路线简图;
(II)若鲸继续以(I)-(2)中的运行路线运动,则鲸经过多少分钟(从放归时计时),可进入前方观测站B的观测范围。()
19. 设A={x|–2≤x≤a},B={y|y=2x+3,且x∈A},C={z|z=x2,且x∈A },若C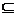 B,求实数a的取值范围.
B,求实数a的取值范围.
18. 已知函数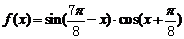 的图象向右平移
的图象向右平移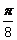 个单位得到函数
个单位得到函数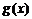 的图象.
的图象.
⑴求函数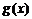 的表达式;
的表达式;
⑵证明当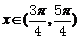 时,经过函数
时,经过函数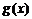 图象上任意两点的直线的斜率恒大于零.
图象上任意两点的直线的斜率恒大于零.
17. 已知A(1,1)为椭圆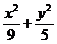 =1内一点,F1为椭圆左焦点,P为椭圆上一动点.求|PF1|+|PA|的最大值和最小值.
=1内一点,F1为椭圆左焦点,P为椭圆上一动点.求|PF1|+|PA|的最大值和最小值.
16. 已知集合A={x|5–x≥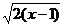 },B={x|x2–ax≤x–a},当B
},B={x|x2–ax≤x–a},当B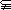 A时,则a的取值范围是
.
A时,则a的取值范围是
.
解析:化简A=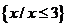 ,化简B=
,化简B=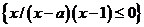 ,画出数轴,结合图像得a≤3。
,画出数轴,结合图像得a≤3。
15.过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线方程是_________
解析:设直线方程为y=kx,圆的方程可化为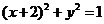 ,因为直线与圆相切,所以d=r,
,因为直线与圆相切,所以d=r,
即: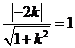 ,解得
,解得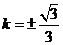 ,结合图像,切点在第三象限,所以直线方程为y=
。
,结合图像,切点在第三象限,所以直线方程为y=
。
14.在(0,2π)内,使sinx>cosx成立的x取值范围为______________
解析:在(0,2π)内分别作出正弦函数y=sinx和余弦函数y=cosx的图像,要使sinx>cosx,只需正弦函数的图像在余弦函数图像的上方,再找出x对应的取值范围为(,)。
13. 定义在区间(―1,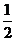 )内的函数
)内的函数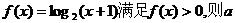 的取值范围是______
的取值范围是______
解析:由已知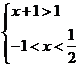 ,解得:
,解得: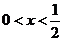
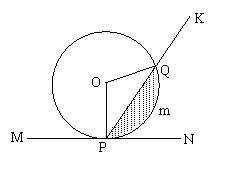
12. 如图,半径为2的⊙O切直线MN于点P,射线PK
从PN出发,绕P点逆时针旋转到PM,旋转过程中PK交⊙O于点Q,若∠POQ为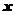 ,弓形PmQ的面积为
,弓形PmQ的面积为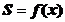 ,那么
,那么 的图象大致是:( )
的图象大致是:( )
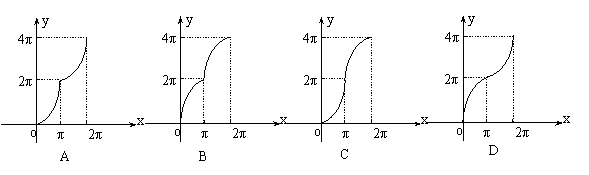
评析:有已知可得当射线PK逆时针旋转的过程中,∠POQ是先迅速增大,到达2π后,角继续增大,但是增加的幅度变慢,有图知C符合要求。
11. 有两个相同的直三棱柱,高为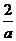 ,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是( ).
,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是( ).
A 0<a<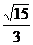 B
B 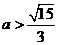
 C
C 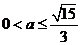 D
D 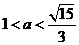
评析:本题考查学生的空间想象能力及树形结合的思想方法,可以通过不同的组合得到不同的几何体,然后分别计算其体积列出不等式可求得0<a<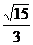 ,故选A。
,故选A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com