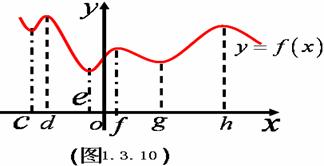
4、引导学生观察图1.3.11，回答以下问题：

(1)找出图中的极点，并说明哪些点为极大值点，哪些点为极小值点？

(2)极大值一定大于极小值吗？

3、通过以上探索，你能归纳出可导函数在某点x0取得极值的充要条件吗？

充要条件：f(x0)=0且点x0的左右附近的导数值符号要相反

2、极值的定义:

我们把点a叫做函数y=f(x)的极小值点，f(a)叫做函数y=f(x)的极小值；

点b叫做函数y=f(x)的极大值点，f(a)叫做函数y=f(x)的极大值。

极大值点与极小值点称为极值点, 极大值与极小值称为极值.

1、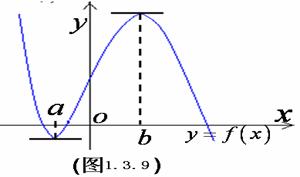观察1.3.9图所表示的y=f(x)的图象，回答以下问题：

(1)函数y=f(x)在a.b点的函数值与这些点附近的函数值有什么关系?

(2) 函数y=f(x)在a.b.点的导数值是多少?

(3)在a.b点附近, y=f(x)的导数的符号分别是什么，并且有什么关系呢?

3、对于这一事例是这样，对其他的连续函数是不是也有这种性质呢？

<二>、探索研讨

2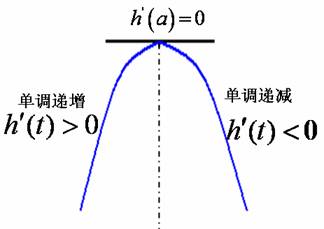．观察图1.3.8 表示高台跳水运动员的高度h随时间t变化的函数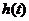=-4.9t2+6.5t+10的图象，回答以下问题

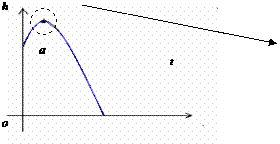
(1)当t=a时，高台跳水运动员距水面的高度最大，那么函数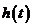在t=a处的导数是多少呢？

(2)在点t=a附近的图象有什么特点？

(3)点t=a附近的导数符号有什么变化规律？

共同归纳:　 函数h(t)在a点处h/(a)=0,在t=a的附近,当t＜a时,函数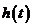单调递增, 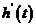＞0;当t＞a时,函数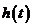单调递减, 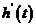＜0,即当t在a的附近从小到大经过a时, 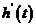先正后负,且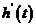连续变化,于是h/(a)=0.

　〈一〉、创设情景，导入新课

1、通过上节课的学习，导数和函数单调性的关系是什么？

(提高学生回答)

回忆函数的单调性与导数的关系，与已有知识的联系

提出问题，激发求知欲

组织学生自主探索，获得函数的极值定义

通过例题和练习，深化提高对函数的极值定义的理解

　　 难点：函数在某点取得极值的必要条件与充分条件

1　 知识与技能

　〈1〉结合函数图象，了解可导函数在某点取得极值的必要条件和充分条件

　〈2〉理解函数极值的概念，会用导数求函数的极大值与极小值

过程与方法

结合实例，借助函数图形直观感知，并探索函数的极值与导数的关系。

情感与价值

感受导数在研究函数性质中一般性和有效性，通过学习让学生体会极值是函数的局部性质，增强学生数形结合的思维意识。