
7.作匀加速直线运动的物体,依次通过A、B、C三点,位移SAB=SBC ,已知物体在AB段的平均速度为3 m/s,在BC段的平均速度大小为6 m/s,那么物体在B点时的即时速度的大小为( )
A.4 m/s B.4.5 m/s C.5 m/s D.5.5 m/s。
6.在平直公路上有甲、乙两辆汽车沿着同一方向做匀加速直线运动,它们的运动速率的平方随位移的变化图象如图所示.则以下说法正确的是
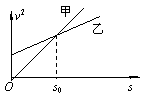 A.甲车的加速度比乙车的加速度大
A.甲车的加速度比乙车的加速度大
B.乙车的加速度比甲车的加速度大
C.两车经过s0位置前运动的时间相同
D.在s0位置甲、乙两车再次相遇
5.一质点从位移原点出发,其运动v-t图像如图所示,则在0至t4时间内( )
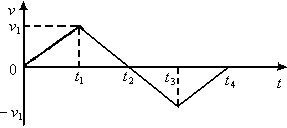
A.速度方向在t1,t3时刻发生改变
B.在t2,t4时刻,质点回到原点
C.在t2时刻,质点离开原点最远
D.在t4时刻,质点离开原点最远
4.物体从静止开始做匀加速运动,测得第n秒内的位移为s,则物体的加速度
A.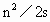 B.
B.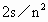
C.2s/(2n-1) D.2s/(2n+1)
3.下列各组物理量中,全部是矢量的是( )
A.质量 位移 速度 B.质量 时间 路程
C.力 位移 速度 D.力 路程 时间
2.一物体自距地面高h处自由下落,则它在离地面多高位置时的即时速度大小等于全程平均速度 ( )
A.h/4 B.h/3 C.3h/4 D.h/2
1.一个质量为m的物体,竖直向下作加速度为3g的匀加速运动,则它受到的重力是( )
A.0 B.mg C.2mg D.3mg
2、思考:已知函数f(x)=ax3+bx2-2x在x=-2,x=1处取得极值,
求函数f(x)的解析式及单调区间。
<五>、课后思考题:
若函数f(x)=x3-3bx+3b在(0,1)内有极小值,求实数b的范围。
已知f(x)=x3+ax2+(a+b)x+1有极大值和极小值,求实数a的范围。
<六>、课堂小结:
函数极值的定义
函数极值求解步骤
一个点为函数的极值点的充要条件。
<七>、作业 P32 5 ① ④
教学反思:
本节的教学内容是导数的极值,有了上节课导数的单调性作铺垫,借助函数图形的直观性探索归纳出导数的极值定义,利用定义求函数的极值.教学反馈中主要是书写格式存在着问题.为了统一要求主张用列表的方式表示,刚开始学生都不愿接受这种格式,但随着几道例题与练习题的展示,学生体会到列表方式的简便,同时为能够快速判断导数的正负,我要求学生尽量把导数因式分解.本节课的难点是函数在某点取得极值的必要条件与充分条件,为了说明这一点多举几个例题是很有必要的.在解答过程中学生还暴露出对复杂函数的求导的准确率比较底,以及求函数的极值的过程板书仍不规范,看样子这些方面还要不断加强训练.
研讨评议:
教学内容整体设计合理,重点突出,难点突破,充分体现教师为主导,学生为主体的双主体课堂地位,充分调动学生的积极性,教师合理清晰的引导思路,使学生的数学思维得到培养和提高,教学内容容量与难度适中,符合学情,并关注学生的个体差异,使不同程度的学生都得到不同效果的收获.
1、求函数f(x)=3x-x3的极值
5、随堂练习:
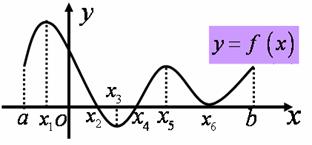
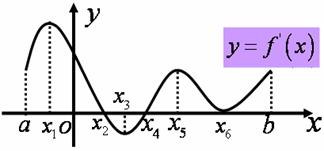
1 如图是函数y=f(x)的函数,试找出函数y=f(x)的极值点,并指出哪些是极大值点,哪些是极小值点.如果把函数图象改为导函数y=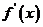 的图象?
的图象?
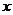 <三>、讲解例题
<三>、讲解例题
求函数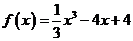 的极值
的极值
 教师分析:①求f/(x),解出f/(x)=0,找函数极点; ②由函数单调性确定在极点x0附近f/(x)的符号,从而确定哪一点是极大值点,哪一点为极小值点,从而求出函数的极值.
教师分析:①求f/(x),解出f/(x)=0,找函数极点; ②由函数单调性确定在极点x0附近f/(x)的符号,从而确定哪一点是极大值点,哪一点为极小值点,从而求出函数的极值.
学生动手做,教师引导
解:∵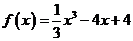 ∴
∴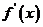 =x2-4=(x-2)(x+2)
=x2-4=(x-2)(x+2)
令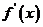 =0,解得x=2,或x=-2.
=0,解得x=2,或x=-2.
下面分两种情况讨论:
当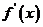 >0,即x>2,或x<-2时;
>0,即x>2,或x<-2时;
当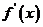 <0,即-2<x<2时.
<0,即-2<x<2时.
当x变化时, 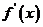 ,f(x)的变化情况如下表:
,f(x)的变化情况如下表:
|
x |
(-∞,-2) |
-2 |
(-2,2) |
2 |
(2,+∞) |
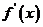 |
+ |
0 |
_ |
0 |
+ |
|
f(x) |
单调递增 |
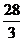 |
 单调递减 单调递减 |
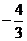 |
单调递增 |
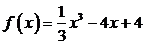 因此,当x=-2时,f(x)有极大值,且极大值为f(-2)=
因此,当x=-2时,f(x)有极大值,且极大值为f(-2)= 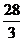 ;当x=2时,f(x)有极
;当x=2时,f(x)有极
小值,且极小值为f(2)= 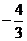
函数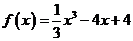 的图象如:
的图象如:
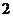 归纳:求函数y=f(x)极值的方法是:
归纳:求函数y=f(x)极值的方法是:
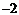 1求
1求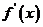 ,解方程
,解方程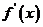 =0,当
=0,当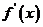 =0时:
=0时:
如果在x0附近的左边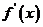 >0,右边
>0,右边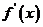 <0,那么f(x0)是极大值.
<0,那么f(x0)是极大值.
如果在x0附近的左边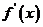 <0,右边
<0,右边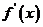 >0,那么f(x0)是极小值
>0,那么f(x0)是极小值
<四>、课堂练习
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com