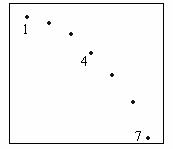
[例8]如图所示，为一平抛物体运动的闪光照片示意图，照片与实际大小相比缩小10倍.对照片中小球位置进行测量得：1与4闪光点竖直距离为1.5 cm，4与7闪光点竖直距离为2.5 cm，各闪光点之间水平距离均为0.5 cm.则

(1)小球抛出时的速度大小为多少?

(2)验证小球抛出点是否在闪光点1处，若不在，则抛出点距闪光点1的实际水平距离和竖直距离分别为多少?(空气阻力不计，g＝10 m/s²)

解析：

(1)设1~4之间时间为T，

竖直方向有：(2.5-1.5)×10^-2×10 m＝gT²

所以T = 0.1 s

水平方向：0.5×10^-2×3×10 m＝v₀T

所以v₀=1.5 m/s

(2)设物体在1点的竖直分速度为v_1y

1~4竖直方向：1.5×10^-2×10 m=v_1yT+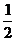gT²

解得v_1y=1 m/s

因v_1y≠0，所以1点不是抛出点

设抛出点为O点，距1水平位移为x m，竖直位移为y m，有

水平方向 x=v₀t

竖直方向：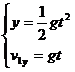

解得t= 0.1 s，

x=0.15 m=15 cm

y=0.05 m=5 cm

即抛出点距1点水平位移为15 cm，竖直位移为5 cm

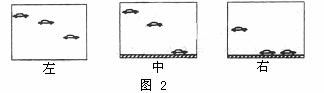
[例9]　 柯受良驾驶汽车飞越黄河，汽车从最高点开始到着地为止这一过程的运动可以看作平抛运动。记者从侧面用照相机通过多次曝光，拍摄到汽车在经过最高点以后的三副运动照片如图2所示，相邻两次曝光时间间隔相等，均为Δt，已知汽车的长度为l，则

A．从左边一幅照片可推算出汽车的水平分速度的大小

B．从左边一幅照片可推算出汽车曾经到达的最大高度

C．从中间一幅照片可推算出汽车的水平分速度的大小和汽车曾经到达的最大高度

D．从右边一幅照片可推算出汽车的水平分速度的大小

解析： 首先应动态的看照片，每幅照片中三个汽车的像是同一辆汽车在不同时刻的像，根据题目的描述，应是由高到低依次出现的，而且相邻两像对应的时间间隔是相等的，均为已知的Δt。

题目中“汽车的长度为l”这一已知条件至关重要，我们量出汽车在照片中的长度，就能得到照片与实际场景的比例，这样照片中各点间的真实距离都能算出。

物理知识告诉我们，汽车在通过最高点后的运动，可抽象为质点的平抛运动，因此水平方向为匀速运动，竖直方向为自由落体运动。

关于水平速度，由于汽车在空中相邻的两个像对应的真实距离能算出，这段运动对应的时间Δt已知，因此由左、中两幅照片中的任意一幅都能算出水平速度。至于右边的一幅，因为汽车在空中的像只有一个，而紧接着的在地上的像不一定是刚着地时的像(汽车刚着地时，可能是在两次拍摄之间)，因此在这个Δt内，可能有一段时间做的已经不是平抛运动了，水平方向不是匀速的。所以用该照片无法计算出水平速度。

关于最大高度，应分析竖直方向，同时对不同照片进行比较。左边一幅，没拍到地面，肯定不能计算最大高度。右边一幅，空中只有一个像，无法分析其自由落体运动。中间一幅，相邻像的两个真实距离均能知道，借用处理纸带的方法，能算出中间那个像对应的速度，进而由自由落体运动的公式算出最高点这个位置的高度，再加上这个位置的离地高度即可得到汽车离地的最大高度。因此该题选A、C。

点评：这是一道很典型的频闪照片的题，给我们很多分析频闪照片的启示：要能看出动态、要关注照片比例、要先确定运动的性质，以便在其指引下分析，多幅照片要进行细致的比较。

研究曲线运动的一般方法就是正交分解法。将复杂的曲线运动分解为两个互相垂直方向上的直线运动。一般以初速度或合外力的方向为坐标轴进行分解。

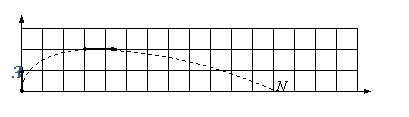[例7] 如图所示，在竖直平面的xoy坐标系内，oy表示竖直向上方向。该平面内存在沿x轴正向的匀强电场。一个带电小球从坐标原点沿oy方向竖直向上抛出，初动能为4J，不计空气阻力。它达到的最高点位置如图中M点所示。求：

⑴小球在M点时的动能E₁。

⑵在图上标出小球落回x轴时的位置N。

⑶小球到达N点时的动能E₂。

解析：⑴在竖直方向小球只受重力，从O→M速度由v₀减小到0；在水平方向小球只受电场力，速度由0增大到v₁，由图知这两个分运动平均速度大小之比为2∶3，因此v₀∶v₁=2∶3，所以小球在M点时的动能E₁=9J。

⑵由竖直分运动知，O→M和M→N经历的时间相同，因此水平位移大小之比为1∶3，故N点的横坐标为12。

⑶小球到达N点时的竖直分速度为v₀，水平分速度为2v₁，由此可得此时动能E₂=40J。

2．应用举例

(1)方格问题

[例3]平抛小球的闪光照片如图。已知方格边长a和闪光照相的频闪间隔T，求：v₀、g、v_c

解析：水平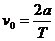方向： 　竖直方向：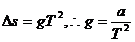

先求C点的水平分速度v_x和竖直分速度v_y，再求合速度v_C：　　

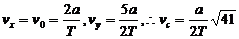
(2)临界问题

典型例题是在排球运动中，为了使从某一位置和某一高度水平扣出的球既不触网、又不出界，扣球速度的取值范围应是多少？

[例4] 已知网高H，半场长L，扣球点高h，扣球点离网水平距离s、求：水平扣球速度v的取值范围。

解析：假设运动员用速度v_max扣球时，球刚好不会出界，用速度v_min扣球时，球刚好不触网，从图中数量关系可得：

；

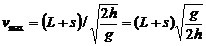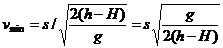
实际扣球速度应在这两个值之间。

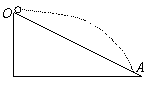[例5]如图所示，长斜面OA的倾角为θ，放在水平地面上，现从顶点O以速度v₀平抛一小球，不计空气阻力，重力加速度为g，求小球在飞行过程中离斜面的最大距离s是多少？

解析：为计算简便，本题也可不用常规方法来处理，而是将速度和加速度分别沿垂直于斜面和平行于斜面方向进行分解。如图15，速度v₀沿垂直斜面方向上的分量为v₁= v₀ sinθ，加速度g在垂直于斜面方向上的分量为a=g cosθ，根据分运动各自独立的原理可知，球离斜面的最大距离仅由和决定，当垂直于斜面的分速度减小为零时，球离斜面的距离才是最大。。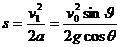

点评：运动的合成与分解遵守平行四边形定则，有时另辟蹊径可以收到意想不到的效果。

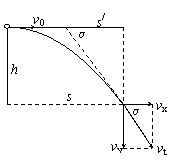(3)一个有用的推论

平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。

证明：设时间t内物体的水平位移为s，竖直位移为h，则末速度的水平分量v_x=v₀=s/t，而竖直分量v_y=2h/t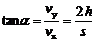， ，　 所以有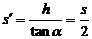

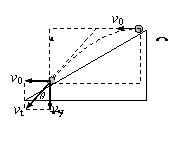[例6] 从倾角为θ=30°的斜面顶端以初动能E=6J向下坡方向平抛出一个小球，则小球落到斜面上时的动能E ^/为______J。

解析：以抛出点和落地点连线为对角线画出矩形ABCD，可以证明末速度v_t的反向延长线必然交AB于其中点O，由图中可知AD∶AO=2∶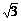，由相似形可知v_t∶v₀=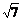∶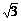，因此很容易可以得出结论：E ^/=14J。

点评：本题也能用解析法求解。列出竖直分运动和水平分运动的方程，注意到倾角和下落高度和射程的关系，有：h=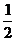gt²，s=v₀t，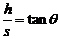

或　 h=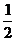v_y t， s=v₀ t　 ，

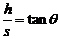
同样可求得v_t∶v₀=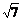∶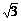，E ^/=14J

当物体初速度水平且仅受重力作用时的运动，被称为平抛运动。其轨迹为抛物线，性质为匀变速运动。平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动这两个分运动。广义地说，当物体所受的合外力恒定且与初速度垂直时，做类平抛运动。

1、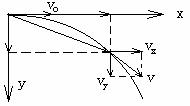平抛运动基本规律

①　 速度：，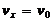

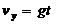
合速度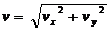

方向 ：tanθ=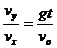

②位移x=v_ot　 y=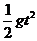

合位移大小：s=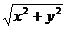　　　　 方向：tanα=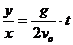

③时间由y=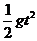得t=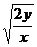(由下落的高度y决定)

④竖直方向自由落体运动，匀变速直线运动的一切规律在竖直方向上都成立。

7．连带运动问题

指物拉绳(杆)或绳(杆)拉物问题。由于高中研究的绳都是不可伸长的，杆都是不可伸长和压缩的，即绳或杆的长度不会改变，所以解题原则是：把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相同求解。

[例1]如图所示，汽车甲以速度v₁拉汽车乙前进，乙的速度为v₂，甲、乙都在水平面上运动，求v₁∶v₂

解析：甲、乙沿绳的速度分别为v₁和v₂cosα，两者应该相等，所以有v₁∶v₂=cosα∶1

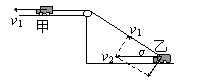[例2] 两根光滑的杆互相垂直地固定在一起。上面分别穿有一个小球。小球a、b间用一细直棒相连如图。当细直棒与竖直杆夹角为α时，求两小球实际速度之比v_a∶v_b

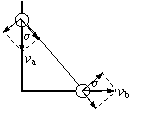解析：a、b沿杆的分速度分别为v_acosα和v_bsinα

∴v_a∶v_b= tanα∶1

6．过河问题

　　 如右图所示，若用v₁表示水速，v₂表示船速，则：

①过河时间仅由v₂的垂直于岸的分量v_⊥决定，即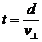，与v₁无关，所以当v₂⊥岸时，过河所用时间最短，最短时间为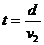也与v₁无关。

②过河路程由实际运动轨迹的方向决定，当v₁＜v₂时，最短路程为d ；当v₁＞v₂时，最短路程程为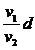(如右图所示)。

5．运动的性质和轨迹

物体运动的性质由加速度决定(加速度得零时物体静止或做匀速运动；加速度恒定时物体做匀变速运动；加速度变化时物体做变加速运动)。

物体运动的轨迹(直线还是曲线)则由物体的速度和加速度的方向关系决定(速度与加速度方向在同一条直线上时物体做直线运动；速度和加速度方向成角度时物体做曲线运动)。

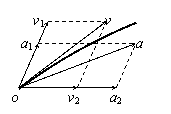两个互成角度的直线运动的合运动是直线运动还是曲线运动？

决定于它们的合速度和合加速度方向是否共线(如图所示)。　　

常见的类型有：

⑴a=0：匀速直线运动或静止。

⑵a恒定：性质为匀变速运动，分为：① v、a同向，匀加速直线运动；②v、a反向，匀减速直线运动；③v、a成角度，匀变速曲线运动(轨迹在v、a之间，和速度v的方向相切，方向逐渐向a的方向接近，但不可能达到。)

⑶a变化：性质为变加速运动。如简谐运动，加速度大小、方向都随时间变化。

4．物体的运动状态是由初速度状态(v₀)和受力情况(F_合)决定的，这是处理复杂运动的力和运动的观点.思路是：

(1)存在中间牵连参照物问题：如人在自动扶梯上行走，可将人对地运动转化为人对梯和梯对地的两个分运动处理。

(2)匀变速曲线运动问题：可根据初速度(v₀)和受力情况建立直角坐标系，将复杂运动转化为坐标轴上的简单运动来处理。如平抛运动、带电粒子在匀强电场中的偏转、带电粒子在重力场和电场中的曲线运动等都可以利用这种方法处理。

3．合运动与分运动的特征：

①等时性：合运动所需时间和对应的每个分运动时间相等

②独立性：一个物体可以同时参与几个不同的分运动，各个分运动独立进行，互不影响。

2．求一个已知运动的分运动，叫运动的分解，解题时应按实际“效果”分解，或正交分解。