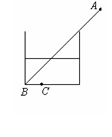
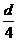[例1]如图所示，一储油圆桶，底面直径与桶高均为d。当桶内无油时，从某点A恰能看到桶底边缘上的某点B。当桶内油的深度等于桶高的一半时，在A点沿AB方向看去，看到桶底上的C点，C、B相距，由此可得油的折射率n=　 ；光在油中传播的速度v=　 m/s。(结果可用根式表示)

答案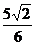　

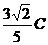
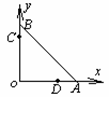(举一反三)、由某种透光物质制成的等腰直角棱镜ABO，两腰长都是16 cm．为了测定这种物质的折射率，将棱镜放在直角坐标系中，并使两腰与ox、oy轴重合，如图所示．从OB边的C点注视A棱，发现A棱的视位置在OA边D点．在C、D两点插大头针，看出C点坐标位置(0，12)D点坐标位置(9，0)，由此可计算出该物质的折射率为　　　　 ．

答案　4/3

[例2]如图所示，为用透明介质做成的空心球，其折射率为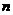，内、外半径分别为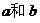,用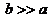内表面涂上能完全吸光的物质，当一束平行光射向此球时被内表面吸收掉的光束在射进空心球前的横截面积是多少？

答案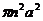

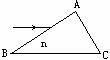[例3]某三棱镜的横截面是一直角三角形，如图所示，∠A=90°，∠B=30°，∠C=60°，棱镜材料的折射率为n，底面BC涂黑，入射光沿平行于底面BC面，经AB面和AC面折射后出射．求(1)出射光线与入射光线延长线间的夹角δ；(2)为使上述入射光线能从AC面出射，折射率n的最大值为多少？

解：画出光路图如图所示。

(1)因为入射光平行于BC面，i=60°

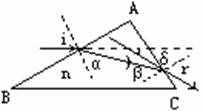由折射定律有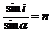，所以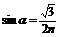

光折到AC面上时，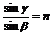

由几何关系可得：A+β=90°

，，

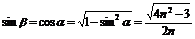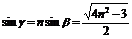(2)要使有光线从AC面射出，应有sinr≤1：即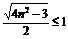，得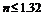

[例4]如图所示，一玻璃柱体的横截面为半圆形，细的单色光束从空气射向柱体的O点(半圆的圆心)产生反射光束1和2，已知玻璃折射率为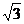，入射角为45⁰(相应的折射角为24⁰),现保持入射光线不变，将半圆柱绕通过O点垂直于图面的轴线顺时针转过15⁰，如图中虚线所示，则：

A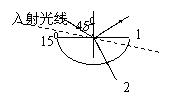．光束1转过15⁰

B． 光束1转过30⁰

C． 光束2转过的角度小于15⁰

D．光束2转过的角度大于15⁰

答案:BC

[例5]如图所示，只含黄光和紫光的复色光束PO，沿半径方向射入空气中的玻璃半圆柱内，被分成两光束OA和OB，若OA和OB分别沿如图所示的方向射出，则：

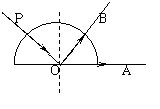A．OA为黄色，OB为紫色

B．OA为紫色，OB为黄色

C．OA为黄色，OB为复色

D．OA为紫色，OB为复色

答案:C

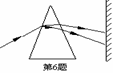[例6]如图所示,一束白光以较大的入射角到三棱镜的一个侧面,从另一个侧面射出,在屏上形成从红到紫的彩色光带.当入射角逐渐减小时

A.红光最先消失.　　　 B.红光紫光同时消失　　

C.紫光最先消失.　　　 D.红光紫光都不消失

答案:C

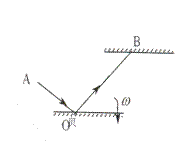
[例7]一点光源发出一束光经一平面镜反射，打在天花

板上，平面镜以角速度ω匀速转动，当入射角为α时，光

斑的运动速度是多少？(已知天花板到平面镜的距离为h)

答案：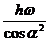

[例7]太阳照在平坦的大沙漠上，我们在沙漠中向前看去，发现前方某处射来亮光，好象太阳光从远处水面射来的一样，我们认为前方有水，但走到该处仍是干燥的沙漠，这种现象在夏天城市中太阳照在沥青路面时也能看到。对此有以下解释：

①这是光的干涉现象；　　　　　②这是光的全反射现象；

③形成原因是越靠近地面处折射率越大；　④形成原因是越靠近地面处折射率越小。

其中正确的是：A、①③；　B、①④；　C、②③；　D、②④。

答案D。

6．光的全反射现象、反射条件、临界角

全反射产生的条件是：(1)光从光密介质射向光疏介质；(2)入射角大于或等于临界角．

两条件必须同时存在，才发生全反射。

临界角是一种特殊的入射角．当光线从某介质射入真空(或空气)时，其临界角的正弦值为。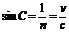

注意：

(1)临界角的含义：折射角为90°时的入射角。

(2)规律：一旦发生全反射,即符合光的反射定律。

(3)光密介质与光疏介质--两个不同的介质。

5．应用(一般方法)：分析光的折射时，一般需作出光路图，以便应用折射规律及光路图中提供的几何关系来解答。

在实际应用中，常见方法是：①三角形边角关系法；②近似法，即利用小角度时，θ≈tanθ≈sinθ的近似关系求解。记住光路是可逆的原理。

(1)折射率的测定

(2)利用折射定律结合几何知识解答的折射问题

(3)多向思维方式理解、应用关键物理量n

①像似深度h^/=H/n

②全反射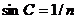

③折射率与波速度的关系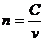

4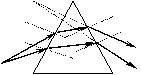．折射时的色散：含有多种颜色的光被分解为单色光的现象叫光的色散。

(1)光通过棱镜时将向棱镜的横截面的底边方向偏折

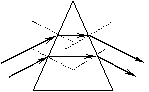(2)通过棱镜成像偏向顶点

(3)实验表面，一束白光进入棱镜而被折射后，在屏上的光斑是彩色的，

说明光在折射时发生了色散。

(4)光的色散规律：红光通过棱镜后偏折的程度比其他颜色的光的要小，

而紫光的偏折程度比其他颜色的光要大。

说明透明物质对于波长不同的光的折射率是不同的。波长越长，折射　　　 率越小。

3．折射率：入射角的正弦与折射角的正弦的比。

(1)折射率的物理意义：表示介质折射光的本领大小的物理量

(2)折射率大小的决定因素--介质、光源(频率)

在其它介质中的速度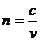，式中n为介质的折射率，n>1，故v<c

注意：

(1)介质的折射率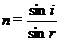是反映介质光学性质的物理量，它的大小由介质本身决定，同时光的频率越高，折射率越大，而与入射角、折射角的大小无关。

(2)某一频率的光在不同介质中传播时,频率不变但折射率不同,所以光速不同,波长也不同(与机械波相同);不同频率的光在同一介质中传播时,折射率不同,所以光速不同,波长也不同(与机械波的区别).频率越高，折射率越大。

2． 光的折射现象，光的折射定律：折射光线与入射光线、法线处于同一平面内，折射光线与入射光线分别位于法线两侧，入射角的正弦与折射角的正弦成正比。

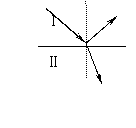注意两角三线的含义

折射率 (光线从介质Ⅰ--介质Ⅱ)

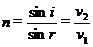
折射现象的光路可逆性

1． 光的反射定律：光从一种介质射到另一种介质的分界面时发生反射。反射光线与入射光线、法线处在同一平面内，反射光线与入射光分别位于法线的两侧。

16.如图所示，匀强磁场的磁感强度B = 0.1T ，矩形线圈的匝数N = 100匝，边长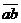= 0.2m 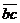，= 0.5m ，转动角速度ω= 100πrad/s ，转轴在正中间。试求：

(1)从图示位置开始计时，该线圈电动势的瞬时表达式；

(2)当转轴移动至ab边(其它条件不变)，再求电动势的瞬时表达式；

(3)当线圈作成半径为r = 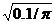的圆形，再求电动势的瞬时表达式。

15.一闭合线圈在匀强磁场中做匀角速转动，线圈转速为240rad/min ，当线圈平面转动至与磁场平行时，线圈的电动势为2.0V 。设线圈从垂直磁场瞬时开始计时，试求：

(1)该线圈电动势的瞬时表达式；

(2)电动势在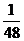s末的瞬时值。

14.将u = 110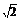sin100πtV的交变电压接到“220V，100W”的灯泡两端，设灯丝的电阻不随温度变化，试求：

(1)流过灯泡电流的最大值；

(2)灯泡发挥的实际功率。