
3.一匀变速直线运动的物体,设全程的平均速度为v1,运动中间时刻的速度为v2,经过全程位移中点的速度为v3,则下列关系正确的是( )
A.v1>v2>v3 B.v1<v2=v3
C.v1=v2<v3 D.v1>v2=v3
2.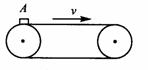 如图所示,水平传送带以不变的速率v
向右运动,将质量为m的物体A轻轻放在其左端,经t秒A的速度也变为v,再经t秒到达右端,则( )
如图所示,水平传送带以不变的速率v
向右运动,将质量为m的物体A轻轻放在其左端,经t秒A的速度也变为v,再经t秒到达右端,则( )
A.前t秒物体作加速运动,后t 秒物体作减速运动
B.A由传送带左端到右端的平均速度为3v/4
C.前t秒A的位移与后t秒位移之为1:2
D.后t秒内A与传送带间无摩擦力
⑴匀变速直线运动中牵涉到的v0、vt、a、s、t五个物理量中,其中只有t是标量,其余都是矢量。一般情况下选取初速度方向为正方向.
⑵在解题过程中,运用变速运动的平均速度公式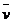 =s/t,这对任何运动都适用;而平均速度公式
=s/t,这对任何运动都适用;而平均速度公式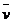 =
=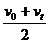 ,只有匀变速直线运动中才能适用。
,只有匀变速直线运动中才能适用。
[典型例题]
[例1] 一物体做匀变速直线运动,某时刻速度大小为4m/s,1秒钟后速度的大小变为10m/s,在这一秒钟内该物体的 ( )
A.位移大小可能小于4m B.位移大小可能大于10m
C.加速度大小可能小于4m/s2 D.加速度大小可能大于10m/s2
[例2] 以v=36 km/h的速度沿平直公路行驶的汽车,遇障碍刹车后获得大小为a=4 m/s2的加速度。刹车后3 s内,汽车走过的路程为( )
A.12 m B.12.5 m
C.90 m D.126 m
[例3] A、B、C三个物体由同一地点同时出发向同一方向做直线运动,它们的速度图象如图所示,问:
(1)A、B、C各做什么运动,加速度各为多少?
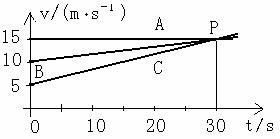 (2)20s末三个物体运动速度的大小关系如何?40s末速度关系又如何?
(2)20s末三个物体运动速度的大小关系如何?40s末速度关系又如何?
(3)P 点的物理意义是什么?
[例4] 如图所示,光滑斜面AE被均分成四段,一物体由A点静止释放,则( )
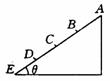 ⑴物体到达各点速度之比vB:vC:vD:vE=1:
⑴物体到达各点速度之比vB:vC:vD:vE=1: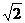 :
: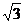 :2
:2
⑵物体到达各点所经历的时间tE=2tB=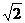 tC=2tD/
tC=2tD/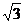
⑶物体从A到E的平均速度等于vB
⑷通过每一段时,其速度增量均相等
A.只有⑴ B.⑴⑵⑶ C.⑵⑷ D.⑶⑷
[例5]有一质点在连续12秒内做匀加速直线运动,在第一个4秒内位移为24m,在最后4秒内位移为56m,则质点的加速度大小为 m/s。
[当堂反馈]
1.甲、乙同时由静止从A处出发,沿直线AB运动,甲先以加速度a1作匀加速运动,经一段时间后,改以加速度a2作匀加速运动,到达B的速度为v ,乙一直以加速度a作匀加速运动,到达B的速度也为v,已知a1>a,则( )
A.甲、乙可能同时到达B
B.甲一定先到达B
C.经过AB中间任一点时甲的速度一定大于乙的速度
D.经过AB直线上某一点时,甲的速度可能小于乙的速度
⑴匀变速直线运动的v-t图象如图所示,其中A描述的是初速度为零的匀加速直线运动;B描述的是初速度为v1的匀加速度直线运动;C描述的初速度为v2的匀减速直线运动。
⑵速度-时间图象的斜率表示加速度。图中A和B的斜率为正,且速度也为正,所以表示物体作匀加速直线运动;C的斜率为负,而速度为正,所以表示C作减速直线运动。
⑶速度-时间图线与横轴t所围的面积表示物体运动的位移,时间轴上方所围的“面积”为正,时间轴下方所围的“面积”为负(对应物体作负速度的反向返回,即位移为负)。
(1)把一段过程分成相等的时间间隔,则
①从运动开始算起,在t秒内、2t秒内、……nt秒内的位移之比为:
d1:d2:d3……:dn=12:22:32……:n2
②从运动开始算起,在连续相等的时间内的位移之比为:
s1:s2:s3……:sn=1:3:5……:(2n-1)
③从运动开始算起,在t秒末、2t秒末、……nt秒末的速度之比为:
v1:v2:v3……:vn=1:2:3……:n
(2)把一段过程分成相等的位移间隔
①从运动开始算起,第一段位移末的速度、第二段位移末的速度……第n段位移末的速度之比为:v1:v2:v3……:vn=1: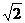 :
: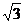 ……:
……: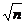
②从运动开始算起,通过连续相同位移所用时间之比为:
t1:t2:t3……:tn=1:(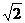 -1):(
-1):(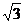 -
-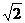 )……:(
)……:(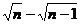 )
)
(1)做匀变速直线运动的物体,如果在各个连续相等的时间t内的位移分别为s1、s2、s3……sn,加速度为a,则△s=s2-s1 = s3-s2=……=sn-sn-1=at2
(2)做匀变速直线运动的物体在某段时间内的平均速度等于这段时间中间时刻的即时速度,即vt/2=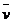 。
。
(3)做匀变速直线运动的物体,在某段位移中点的即时速度等于初速度和末速度平方和一半的平方根,即vs/2=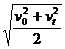 。
。
基本公式有四条:
(1) 速度公式:vt=v0+at
(2)位移公式:s=v0t+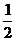 at2
at2
(3)速度位移关系公式:vt2-v02=2as
(4)平均速度公式: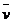 =
=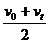
12.核聚变能是一种具有经济性能优越、安全可靠、无环境污染等优势的新能源。近年来,受控核聚变的科学可行性已得到验证,目前正在突破关键技术,最终将建成商用核聚变电站。一种常见的核聚变反应是由氢的同位素氘(又叫重氢)和氚(又叫超重氢)聚合成氦,并释放一个中子了。若已知氘原子的质量为2.0141u,氚原子的质量为3.0160u,氦原子的质量为4.0026u,中子的质量为1.0087u,1u=1.66×10-27kg。
⑴写出氘和氚聚合的反应方程。
⑵试计算这个核反应释放出来的能量。
⑶若建一座功率为3.0×105kW的核聚变电站,假设聚变所产生的能量有一半变成了电能,每年要消耗多少氘的质量?
(一年按3.2×107s计算,光速c=3.00×108m/s,结果取二位有效数字)
11.自然界中的物体由于具有一定的温度,会不断地向外辐射电磁波,这种辐射因与温度有关,称为热辐射。热辐射具有如下特点:(1)辐射的能量中包含各种波长的电磁波;(2)物体温度越高,单位时间内从物体表面单位面积上辐射的能量越大;(3)在辐射的总能量中,各种波长所占的百分比不同。
处在一定温度的物体在向外辐射电磁能量的同时,也要吸收由其他物体辐射的电磁能量,如果它处在平衡状态,则能量保持不变。若不考虑物体表面性质对辐射与吸收的影响,我们定义一种理想的物体,它能100%地吸收入射到其表面的电磁辐射,这样的物体称为黑体。单位时间内从黑体表面单位面积辐射的电磁波的总能量与黑体绝对温度的四次方成正比,即P0=σT4,其中常量σ=5 .67×10-8W/(m•K4)
在下面的问题中,把研究对象都简单地看作黑体。
有关数据及数学公式:太阳半径Rs = 696000Km,太阳表面温度T = 5770K,火星半径r = 3395Km。已知球面积S = 4πR2,其中R为球半径。
(1) 太阳热辐射能量的绝大多数集中在波长为2×10-7-1×10-5m范围内,求相应的频率范围。
(2) 每小时从太阳表面辐射的总能量为多少?
(3) 火星受到来自太阳的辐射可认为垂直到面积为πr2(r为火星半径)的圆盘上。已知太阳到火星的距离约为太阳半径的400倍,忽略其他天体及宇宙空间的辐射,试估算火星的平均温度。
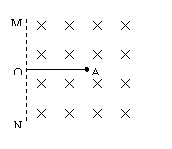
10.如下图所示,一个有界的匀强磁场,磁感应强度B=0.50T,磁场方向垂直于纸面向里,MN是磁场的左边界。在磁场中A处放一个放射源,内装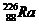 (镭),
(镭),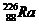 放出某种射线后衰变成Rn(氡)。试写出:
放出某种射线后衰变成Rn(氡)。试写出: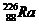 衰变的方程,若A距磁场的左边界MN的距离OA=1.0m,放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的质量较小的粒子,此时接收器位置距经过OA的直线1.0m,由此可以推断出一个静止镭核Ra衰变时放出的能量是多少?保留两位有效数字(取1u=1.6×10-27kg,电子电量e=1.6×10-19c)
衰变的方程,若A距磁场的左边界MN的距离OA=1.0m,放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的质量较小的粒子,此时接收器位置距经过OA的直线1.0m,由此可以推断出一个静止镭核Ra衰变时放出的能量是多少?保留两位有效数字(取1u=1.6×10-27kg,电子电量e=1.6×10-19c)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com