
17. 解:(1)由已知得 ,∵
,∵ ,∴
,∴ .
……………2分
.
……………2分
∵ 、
、 是方程
是方程 的两个根,∴
的两个根,∴ .
……………4分
.
……………4分
∴ ,
, …………………………………………………………6分
…………………………………………………………6分
(2) 的可能取值为0,100,200,300,400
的可能取值为0,100,200,300,400
 ,
, ,
,
 ,
, ,
,
 .
………………………………………………………9分
.
………………………………………………………9分
即 的分布列为:
的分布列为:
 |
0 |
100 |
200 |
300 |
400 |
 |
 |
 |
 |
 |
 |
故 …………12分
…………12分
16.解:(1)由 …………………4分
…………………4分
 为
为 的内角,
的内角, …………………………………6分
…………………………………6分
(2)由余弦定理:
即 ………………………………………………………10分
………………………………………………………10分
又 . …………………………………………………12分
. …………………………………………………12分
13. . 14.
. 14.  15.
15. 
9解:记第n次运算的结果为 ,则
,则 解得
解得 ,由
,由 答案:4
答案:4
10解: . 答案:20
. 答案:20
 11解:画出二元一次不等式组表示的平面区域,由角点法得z的最大值为1. 答案:1
11解:画出二元一次不等式组表示的平面区域,由角点法得z的最大值为1. 答案:1
12解:如图,令 作平行四边形OBDC,则
作平行四边形OBDC,则
 答案:
答案: 
13解: 点P的直角坐标为(-1,0), 则过点P且垂直极轴的直线的直角坐标方程为
 ,极坐标方程为
,极坐标方程为 . 答案:
. 答案: 
14解:由题可知, 
 答案:
答案:
15解:由题可得,
答案: 
9.4;
10.20;
11.1;
12. ;
;
1解:
2解:
3解:

4解:
5解:
6解:
7解:圆锥形漏斗中液面开始下降的速度慢,后来下降的速度越来越快。故选B;
 8解:由题可知,
8解:由题可知,
 在
在 上恒成立,即
上恒成立,即
故
如图,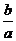 即为图中阴影部分的点与原点连线的
即为图中阴影部分的点与原点连线的
斜率.故选A
21.(本题满分14分)
已知函数

(1)求 的值;
的值;
(2)已知数列 ,求数列
,求数列 的通项公式;
的通项公式;
(3)求证: .
.
惠州市2010届高三摸底考试
数学(理科)
|
20.(本题满分14分)
 已知定点A(-2,0),动点B是圆
已知定点A(-2,0),动点B是圆 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T, 且满足 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.
19.(本题满分14分)
已知 ,直线
,直线 与函数
与函数 的图象都相切于点
的图象都相切于点 .
.
(1)求直线 的方程及
的方程及 的解析式;
的解析式;
(2)若 (其中
(其中 是
是 的导函数),求函数
的导函数),求函数 的值域.
的值域.
18.(本题满分14分)
 已知直三棱柱
已知直三棱柱 D是AB的中点.
D是AB的中点.
(1)求证:CD⊥平面ABB1A1;
(2)求二面角D-A1C-A的正切值;
(3)求点C1到平面A1CD的距离.
17.(本题满分12分)
某种家用电器每台的销售利润与该电器的无故障使用时间T (单位:年)有关.若T≤1,则销售利润为0元;若1<T≤3,则销售利润为100元;若T>3,则销售利润为200元.设每台该种电器的无故障使用时间T≤1,1<T≤3及T>3这三种情况发生的概率分别为p1,p2,p3,又知p1,p2是方程 的两个根,且p2=p3.
的两个根,且p2=p3.
(1)求p1,p2,p3的值;
(2)记 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求 的期望.
的期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com