5.有三种材质不同的型材，他们分别由纯铁、铜、铝制成。这三者中，强度最大的是：(　　 )

A.铜型材　　　　　 B.纯铁型材　　　　 C.铝型材　　　　　 D.不能确定

4.在日常生活中重心的位置是决定结构稳定性的一个重要因素，以下哪一种结构不是利用降低重心高度来实现其稳定状态的(　　 )

A.自行车的支撑架　 B.儿童陀螺玩具　 C.电风扇的底座　　 D.不倒翁玩具

3.钢筋混凝土梁中比无钢筋的水泥梁的(　　 )强度更强

A.抗弯　　　　　　 B.抗拉　　　　　 C.抗压　　　　　　 D.抗剪

1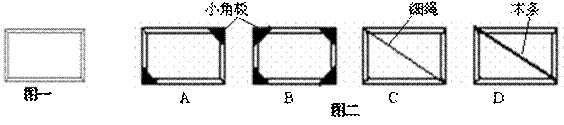．高二某班的同学用木条和乳胶等做了一个长方形的奖状框用来放置他们获得的荣誉奖状(如图一)。他们发现这个结构容易变形，便提出了如下四种改进方案(如图二)。你认为最不合适的方案是：(　　 )

2．如图所示的结构中，不属于薄壳结构的是：(　　 )

A．安全帽　　　　 B．电饭煲　　　　　　　 C．窗台护栏　　　　　　 D．天文台穹顶

13．(20分)(2010·吉林检测)已知函数f(x)＝ax²+4x+b(a<0，a，b∈R)，设关于x的方程f(x)＝0的两实根为x₁、x₂，方程f(x)＝x的两实根为α，β.

(1)若|α－β|＝1，求a、b的关系式；

(2)若α<1<β<2，求证(x₁+1)(x₂+1)<7.

(1)解：由f(x)＝x得ax²+3x+b＝0(a<0，a，b∈R)有两个不等实根为α、β，

∴Δ＝9－4ab>0，α+β＝－，α·β＝

由|α－β|＝1得(α－β)²＝1，

即(α+β)²－4αβ＝－＝1，

∴9－4ab＝a²，即a²+4ab＝9(a<0，a，b∈R)

(2)证明：∵α+β＝－，α·β＝，x₁+x₂＝－，

x₁·x₂＝，

∴x₁+x₂＝(α+β)，x₁·x₂＝αβ

则(x₁+1)(x₂+1)＝x₁x₂+x₁+x₂+1＝αβ+(α+β)+1

又由α<1<β<2

∴α+β<3∴αβ<2，∴(α+β)<4.

∴αβ+(α+β)+1<7.综上所述，(x₁+1)(x₂+1)<7.

12．(15分)设f(x)＝x²+ax+3－a，若f(x)在闭区间[－2,2]上恒为非负数，求实数a的取值范围．

解：f(x)＝x²+ax+3－a＝²+3－a－.

f(x)≥0在x∈[－2,2]上恒成立，即f(x)在[－2,2]上的最小值非负．

(1)当－<－2，即a>4时，y_min＝f(－2)＝7－3a，由7－3a≥0，得a≤，这与a>4矛盾，此时a不存在；

(2)当－2≤－≤2，即－4≤a≤4时，y_min＝f＝3－a－，由3－a－≥0，得－6≤a≤2，此时－4≤a≤2；

(3)当－>2，即a<－4时，y_min＝f(2)＝7+a，由7+a≥0，得a≥－7，此时－7≤a<－4.

综上，所求a的范围是[－7,2]．

11．(15分)已知二次函数f(x)的二次项系数为a，且不等式f(x)>－2x的解集为(1,3)．

(1)若方程f(x)+6a＝0有两个相等的根，求f(x)的解析式；

(2)若f(x)的最大值为正数，求实数a的取值范围．

解：本题主要考查二次函数、方程的根与系数关系，考查运用数学知识解决问题的能力．

(1)∵f(x)+2x>0的解集为(1,3)．

∴f(x)+2x＝a(x－1)(x－3)，且a<0，因而

f(x)＝a(x－1)(x－3)－2x＝ax²－(2+4a)x+3a.　 ①

由方程f(x)+6a＝0，得ax²－(2+4a)x+9a＝0.②

∵方程②有两个相等的根，∴Δ＝[－(2+4a)]²－4a·9a＝0，即5a²－4a－1＝0.解得a＝1或a＝－.　　 　　　　　　　　　　　　　　

由于a<0，舍去a＝1，将a＝－代入①得

f(x)的解析式为f(x)＝－x²－x－.

(2)由f(x)＝ax²－2(1+2a)x+3a

＝a²－

及a<0，可得f(x)的最大值为－.

由

解得a<－2－或－2+<a<0.

故当f(x)的最大值为正数时，实数a的取值范围是

(－∞，－2－)∪(－2+，0)．

10．(2008·浙江高考)已知t为常数，函数y＝|x²－2x－t|在区间[0,3]上的最大值为2，则t＝________.

解析：令m＝x²－2x∈[－1,3]，y＝|m－t|的最大值在m＝－1或m＝3时取得，|－1－t|²－|3－t|²＝8(t－1)，当t≥1时，y_max＝|t+1|＝t+1＝2，∴t＝1.

当t<1时，y_max＝|3－t|＝3－t＝2，t＝1(舍去)，综合分析得t＝1.

答案：1

9．若关于x的方程3x²－5x+a＝0的一个根在(－2,0)内，另一个根在(1,3)内，则a的取值范围是________．

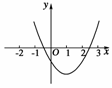
图1

解析：设f(x)＝3x²－5x+a(如图1所示)，则f(x)＝0的两根分别在(－2,0)、(1,3)内的充要条件是

解之，得－12<a<0.

答案：(－12,0)

8．已知A＝[1，b](b>1)，对于f(x)＝(x－1)²+1，当x∈A时，f(x)∈A，则b的值是__________．

解析：x∈[1，b]时，f(x)是增函数，故x＝b时，f(x)取最大值，即f(b)＝b，得(b－1)²+1＝b，解得b＝3或b＝1(舍去)．

答案：3