
1、(绍兴市2008学年第一学期统考数学试题)已知集合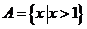 ,集合B=
,集合B= ;(1)当
;(1)当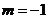 时,求
时,求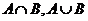 ;(2)若
;(2)若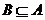 ,求
,求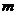 的取值范围.
的取值范围.
解析:(1)当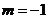 时,
时,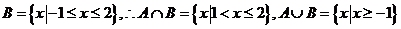 ;
;
(2)若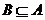 ,则
,则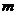 的取值范围为
的取值范围为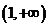 .
.
1.(温州市十校联合体2008学年高三第一学期期初联考 08.8数学试卷(理科))
设集合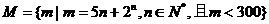 ,则集合M中所有元素的和为 690
,则集合M中所有元素的和为 690
2(宁波市2008学年度第一学期期末试卷高三数学(理科))
若命题“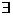 x∈R, 使x2+ax+1<0”是真命题,则实数a的取值范围为 ▲ .
x∈R, 使x2+ax+1<0”是真命题,则实数a的取值范围为 ▲ . 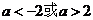
3(嘉兴市2008年高中学科基础测试(理科)数学试题卷2009.1)
命题“∨x∈R, ”的否定是 ▲ ..x0∈R,
”的否定是 ▲ ..x0∈R,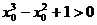 .
.
4(台州市2008学年第一学期高三年级期末质量评估试题
|
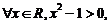 则命题P的否定 ▲ .
则命题P的否定 ▲ . 
5(嘉兴市2008年高中学科基础测试(文科)数学试题卷2009.1)
已知命题p:“对任意的x∈R, ”,则命题┐p是 ▲ .
”,则命题┐p是 ▲ .
x∈R,x3-x2+1>0.
6(台州市2008学年第一学期高三年级期末质量评估试题数 学(文))命题“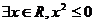 ”的否定是 ▲
.
”的否定是 ▲
. 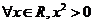
5.(2008学年第一学期十校高三期末联考数学试题(文))祝 同 学 们 新 年 快 乐
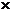 乐
乐

祝 祝 祝 祝 祝 祝 祝 祝 祝
在上面式子中“祝”表示数字_ 。
答案:1
4.(2008学年第一学期期中杭州七校高三联考数学试题)在下面等号右侧两个分数的分母括号内,各填上一个正数,并使这两个正数的和最小:
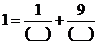 (两个空格全对才给分)
(两个空格全对才给分)
答案:4,12
3.(2008-2009学年上学期期中高三数学试题(文))设集合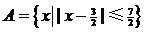 ,
,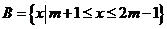 ,若
,若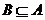 ,则实数
,则实数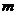 的取值范围
的取值范围
答案: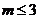
2.(宁波市2008学年度第一学期高三期末数(理))若命题“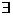 x∈R, 使x2+ax+1<0”是真命题,则实数a的取值范围为
.
x∈R, 使x2+ax+1<0”是真命题,则实数a的取值范围为
.
答案: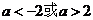
1.(学军中学2008-2009学年上学期高三期中数学试题(理))
设集合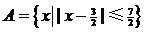 ,
,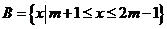 ,若
,若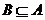 ,则实数
,则实数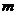 的取值范围
的取值范围
答案: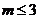
75、(江苏省前黄高级中学2008届高三调研)在正方体ABCD-A1B1C1D1中,E、F分
别是BB1、CD的中点.
(1)求证AE⊥D1F;
(2)证明平面AED⊥平面A1FD1.
解:(1)取AB的中点G,则易证得A1G∥D1F.
又正方形A1ABB1中,E、G分别是相应边的中点,
∴A1G⊥AE,
∴D1F⊥AE.
(2)由正方体可知:A1 D1⊥面A1ABB1,∴A1D1⊥AE .
又由(1)已证:D1F⊥AE.
∵A1D1∩D1F= D1,
∴AE⊥平面A1FD1 .
又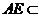 平面AED,
平面AED,
∴平面AED⊥平面A1FD1 .
74、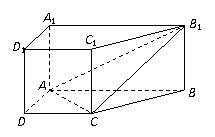 (江苏省南通市2008届高三第二次调研考试)直棱柱
(江苏省南通市2008届高三第二次调研考试)直棱柱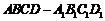 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,
∠BAD=∠ADC=90°, .
.
(Ⅰ)求证:AC⊥平面BB1C1C;
(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与
平面ACB1都平行?证明你的结论.
证明:(Ⅰ) 直棱柱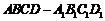 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD, BB1⊥AC. ………………2分
BB1⊥AC. ………………2分
又 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°, ,
,
∴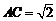 ,∠CAB=45°,∴
,∠CAB=45°,∴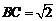 ,
, BC⊥AC.………………………………5分
BC⊥AC.………………………………5分
又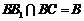 ,
,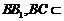 平面BB1C1C,
平面BB1C1C, AC⊥平面BB1C1C. ………………7分
AC⊥平面BB1C1C. ………………7分
(Ⅱ)存在点P,P为A1B1的中点. ……………………………………………………………8分
证明:由P为A1B1的中点,有PB1‖AB,且PB1=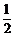 AB.……………………………………9分
AB.……………………………………9分
又∵DC‖AB,DC=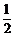 AB,
AB, DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1,
∴DC PB1为平行四边形,从而CB1∥DP.……………………………………………11分
又CB1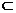 面ACB1,DP
面ACB1,DP 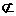 面ACB1,
面ACB1, DP‖面ACB1.………………………………13分
DP‖面ACB1.………………………………13分
同理,DP‖面BCB1.……………………………………………………………………14分
评讲建议:
本题主要考查线面平行、垂直的的判定和证明等相关知识,第一小题要引导学生挖掘直角梯形ABCD中BC⊥AC,第二小题,要求学生熟练掌握一个常用结论:若一直线与两相交平面相交,则这条直线一定与这两平面的交线平行;同时注意问题的逻辑要求和答题的规范性,这里只需要指出结论并验证其充分性即可,当然亦可以先探求结论,再证明之,这事实上证明了结论是充分且必要的.
变题:
求证:(1)A1B⊥B1D;(2)试在棱AB上确定一点E,使A1E∥平面ACD1,并说明理由.
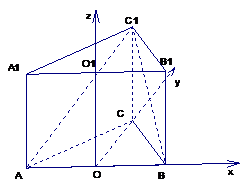
73、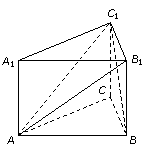 (江苏省南京市2008届高三第一次调研测试)如图,在正三棱柱ABC–A1B1C1中,AB = 2,AB1⊥BC1
(江苏省南京市2008届高三第一次调研测试)如图,在正三棱柱ABC–A1B1C1中,AB = 2,AB1⊥BC1
(1)求BB1的长;
(2)求二面角A1–AB1–C1的余弦值.
解:(1)分别取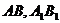 中点
中点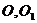 ,连结
,连结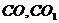 .
.
在正三棱柱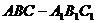 中,四边形
中,四边形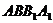 为矩形,
为矩形,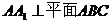 .
.
 分别为
分别为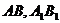 中点,
中点,

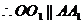 ,
,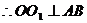 .
.
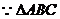 为正三角形,
为正三角形, 为
为 中点.
中点.
 ,
,
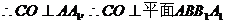

分别以
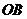 ,
, ,
,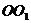 所在直线为
所在直线为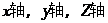 .
.
建立如图的空间直角坐标系……………………………………2分.
设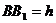 ,
,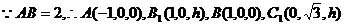 .
.

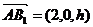 ,
,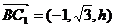
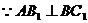
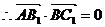 即:
即:
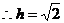 即:
即: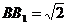 ……………………………………5分.
……………………………………5分.
(2)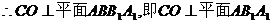
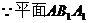 的一个法向量是
的一个法向量是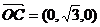 …………………7分.
…………………7分.
设平面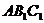 的法向量为
的法向量为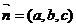
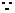
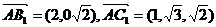 ,
,
又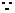
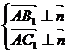
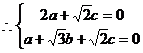 解得:
解得: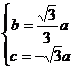
不妨设 ,则平面
,则平面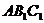 的一个法向量
的一个法向量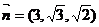 …………10分
…………10分
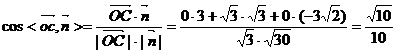
 二面角
二面角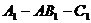 的余弦值是
的余弦值是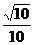 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com