
4、一名运动员在百米赛跑中,测得他在50米处的速度是6m/s,16s末到达终点时的速度为7.5m/s,他在全程内平均速度的大小是 ( )
A. 6m/s B. 6.25m/s C.6.75m/s D.7.5m/s
3、一个质点沿半径为R的圆周运动一周,回到原地,它在运动过程中路程、位移大小的最大值分别是 ( )
A.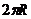 2R B. 2R
2R B. 2R 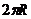 C.2R 2R D.
C.2R 2R D. 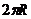 0
0
2、关于速度和加速度的关系,正确的是 ( )
A.速度变化大,加速度就大 B.速度变化越快,加速度越大
C.加速度方向保持不变,速度方向也不变 D.加速度数值不断变小,速度也不断变小
1、下列情况的物体,可以看作质点的是 ( )
A. 研究绕地球飞行的航天飞机; B.研究汽车后轮各点运动时的车轮
C.水平地面上放一只木箱,用力推它沿直线滑动,研究其运动情况的木箱
D.研究自转时的地球
2.超几何分布列的简单应用.
1.超几何分布的特点;
2.练习:课本第51页练习第1,2题.
1.例题:
例1.高三(1)班的联欢会上设计了一项游戏:在一个口袋中装有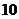 个红球,
个红球,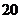 个白球,这些球除颜色外完全相同.现一次从中摸出
个白球,这些球除颜色外完全相同.现一次从中摸出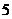 个球,
个球,
(1)若摸到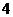 个红球
个红球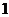 个白球的就中一等奖,求中一等奖的概率.
个白球的就中一等奖,求中一等奖的概率.
(2)若至少摸到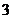 个红球就中奖,求中奖的概率.
个红球就中奖,求中奖的概率.
解:(1)若以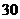 个球为一批产品,其中红球为不合格产品,随机抽取
个球为一批产品,其中红球为不合格产品,随机抽取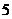 个球,
个球,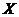 表示取到的红球数,则
表示取到的红球数,则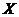 服从超几何分布
服从超几何分布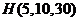 .
.
由公式得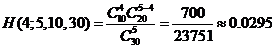 ,
,
所以获一等奖的概率约为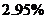 .
.
(2)根据题意,设随机变量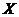 表示“摸出红球的个数”,则
表示“摸出红球的个数”,则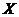 服从超几何分布
服从超几何分布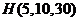 ,
,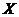 的可能取值为
的可能取值为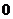 ,
,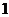 ,
,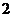 ,
,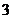 ,
,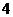 ,
,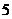 ,根据公式可得至少摸到
,根据公式可得至少摸到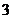 个红球的概率为:
个红球的概率为:
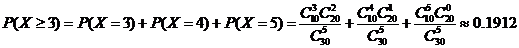 ,
,
故中奖的概率为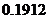 .
.
例2.生产方提供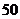 箱的一批产品,其中有
箱的一批产品,其中有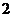 箱不合格产品.采购方接收该批产品的准则是:从该批产品中任取
箱不合格产品.采购方接收该批产品的准则是:从该批产品中任取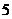 箱产品进行检测,若至多有
箱产品进行检测,若至多有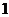 箱不合格产品,便接收该批产品.问:该批产品被接收的概率是多少?
箱不合格产品,便接收该批产品.问:该批产品被接收的概率是多少?
解:以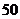 箱为一批产品,从中随机抽取
箱为一批产品,从中随机抽取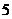 箱,用
箱,用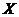 表示“
表示“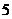 箱中不合格产品的箱数”,则
箱中不合格产品的箱数”,则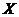 服从超几何分布
服从超几何分布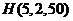 .这批产品被接收的条件是
.这批产品被接收的条件是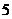 箱中没有不合格的箱或只有
箱中没有不合格的箱或只有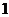 箱不 合格,所以被接收的概率为
箱不 合格,所以被接收的概率为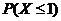 ,即
,即 .
.
答:该批产品被接收的概率是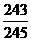 (约为
(约为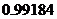 ).
).
说明:(1)在超几何分布中,只要知道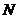 、
、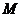 和
和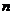 ,就可以根据公式,求出
,就可以根据公式,求出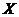 取不同
取不同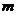 值时的概率
值时的概率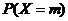 ,从而列出
,从而列出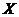 的分布列.
的分布列.
(2)一旦掌握了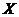 的分布列,就可以算出相应试验的很多事件的概率,从而就完全掌握了该试验.
的分布列,就可以算出相应试验的很多事件的概率,从而就完全掌握了该试验.
思考:该批产品中出现不合格产品的概率是多少?
例3.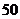 张彩票中只有
张彩票中只有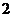 张中奖票,今从中任取
张中奖票,今从中任取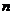 张,为了使这
张,为了使这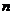 张彩票里至少有一张中奖的概率大于
张彩票里至少有一张中奖的概率大于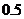 ,
,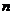 至少为多少?
至少为多少?
解:设随机变量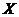 表示“抽出中奖票的张数”,则
表示“抽出中奖票的张数”,则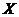 服从超几何分布
服从超几何分布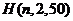 ,根据公式可得至少有一张中奖的概率
,根据公式可得至少有一张中奖的概率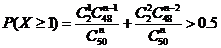 ,解得
,解得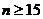 .
.
答: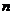 至少为
至少为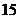 张.
张.
从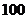 件产品中随机抽取
件产品中随机抽取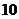 件有
件有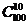 种等可能基本事件.
种等可能基本事件.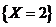 表示的随机事件是“取到
表示的随机事件是“取到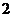 件不合格品和
件不合格品和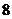 件合格品”,依据分步计数原理有
件合格品”,依据分步计数原理有 种基本事件,根据古典概型,
种基本事件,根据古典概型,
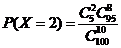 .
.
类似地,可以求得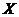 取其他值时对应的随机事件的概率,从而得到不合格品数
取其他值时对应的随机事件的概率,从而得到不合格品数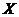 的概率分布如下表所示:
的概率分布如下表所示:
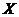
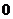
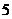
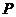
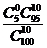
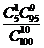
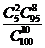
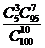
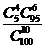
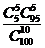
对一般情形,一批产品共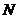 件,其中有
件,其中有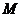 件不合格品,随机取出的
件不合格品,随机取出的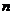 件产品中,不合格品数
件产品中,不合格品数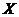 的分布如下表所示:
的分布如下表所示:
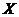 |
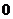 |
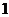 |
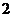 |
… |
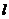 |
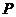 |
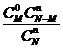 |
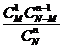 |
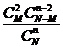 |
… |
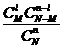 |
其中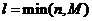 .
.
一般地,若一个随机变量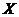 的分布列为
的分布列为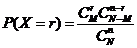 ,
,
其中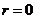 ,
,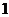 ,
,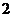 ,
,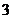 ,…,
,…,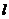 ,
,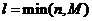 ,则称
,则称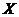 服从超几何分布,记为
服从超几何分布,记为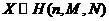 ,并将
,并将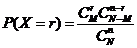 记为
记为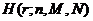 .
.
说明:(1)超几何分布的模型是不放回抽样; (2)超几何分布中的参数是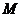 ,
,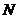 ,
,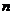 .
.
以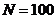 ,
,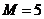 ,
,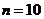 为例,研究抽取
为例,研究抽取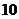 件产品中不合格品数
件产品中不合格品数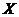 的概率分布.
的概率分布.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com