14．如图40所示，OACO为置于水平面内的光滑闭合金属导轨，O、C处分别接有短电阻丝，R₁＝4　 Ω，R₂＝8 Ω(导轨其他部分电阻不计)，导轨OAC的形状满足方程y＝2sinx(单位：m)，磁感应强度B＝0.2 T的匀强磁场方向垂直于导轨平面，足够长的金属棒在水平外力F作用下，以恒定的速率v＝5.0 m/s水平向右在导轨上从O点滑动到C点，棒与导轨接触良好且始终保持与OC导轨垂直，不计棒的电阻．求：

(1)外力F的最大值．

(2)金属棒在导轨上运动时电阻丝R₁上消耗的最大功率．

(3)在滑动过程中通过金属棒的电流I与时间t的关系．

解析：(1)金属棒匀速运动F_外＝F_安，据E＝BLv

I＝，则F_外＝BIL＝

当L达到最大，即r＝时，L_max＝2sin＝2 m

R_总＝＝ Ω，则

F_max＝＝0.3 N

(2)P₁＝＝＝1 W

(3)金属棒与导轨接触点间的长度随时间变化

L＝2sinx　 m

且x＝vt，E＝BLv，则

I＝＝2sinvt＝sint A

答案：(1)0.3 N　(2)1 W　(3)I＝sint

13．如图39甲所示，足够长的光滑平行金属导轨MN、PQ固定在同一水平面上，两导轨间距L＝0.30 m．导轨电阻忽略不计，其间连接有定值电阻　 R＝0.40　 Ω.导轨上静置一质量m＝0.10 kg、电阻r＝0.20 Ω的金属杆ab，整个装置处于磁感应强度B＝0.50 T的匀强磁场中，磁场方向竖直向下．用一外力F沿水平方向拉金属杆ab，使它由静止开始运动(金属杆与导轨接触良好并保持与导轨垂直)，电流传感器(不计传感器的电阻)可将通过R的电流I即时采集并输入计算机，获得电流I随时间t变化的关系如图乙所示．求金属杆开始运动2.0 s时：

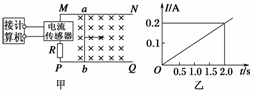
图39

(1)金属杆ab受到安培力的大小和方向；

(2)金属杆的速率；

(3)对图象分析表明，金属杆在外力作用下做匀加速运动，加速度大小a＝0.40 m/s²，计算2.0 s时外力F做功的功率．

解析：(1)由图乙可知2.0 s时通过金属杆ab的电流为0.2 A.

设此时金属杆受到的安培力为F_安，根据安培力公式有

F_安＝BIL

解得：F_安＝3.0×10^－2　 N，方向水平向左

(2)设金属杆产生的感应电动势为E，根据闭合电路欧姆定律I＝

解得：E＝0.12 V

设金属杆在2.0 s时的速率为v₁，则E＝BLv₁

解得：v₁＝0.80 m/s.

(3)根据牛顿第二定律F－F_安＝ma

解得：在2.0 s时拉力F＝7.0×10^－2 N

设2.0 s时拉力F做功的功率为P，则P＝Fv₁

解得：P＝5.6×10^－2 W.

答案：(1)3.0×10^－2 N　水平向左　(2)0.8 m/s

(3)5.6×10^－2 W

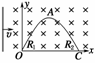
图40

12．在拆装某种大型电磁设备的过程中，需将设备内部处于强磁场中的线圈先闭合，然后再提升直至离开磁场．操作时通过手摇轮轴A和定滑轮O来提升线圈．假设该线圈可简化为水平长为L、上下宽度为d的矩形线圈，其匝数为n，总质量为M，总电阻为R.磁场的磁感应强度大小为B，方向垂直纸面向里，如图38所示．开始时线圈的上边缘与有界磁场的上边缘平齐．若转动手摇轮轴A，在时间t内把线圈从图示位置匀速向上拉出磁场．不考虑摩擦影响，求此过程中

(1)流过线圈中导线横截面的电荷量．

(2)人至少要做多少功．

解析：(1)线圈匀速提升的速度v＝

线圈中感应电动势E＝nBLv

产生的感应电流I＝

流过导线横截面的电荷量q＝It

联立以上各式解得q＝n

(2)匀速提升过程中，人要克服重力和安培力做功

即W＝W_G+W_B，又W_G＝Mgd，W_B＝nBILd

解得W＝Mgd+

答案：(1)n　(2)Mgd+

11．如图37所示，将两条倾角θ＝30°，宽度L＝1 m的足够长的“U”形平行的光滑金属导轨固定在磁感应强度B＝1 T，范围足够大的匀强磁场中，磁场方向垂直于斜面向下．用平行于导轨的牵引力拉一质量m＝0.2 kg，电阻R＝1 Ω放在导轨上的金属棒ab，使之由静止沿轨道向上运动，牵引力的功率恒为P＝6 W，当金属棒移动s＝2.8 m时，获得稳定速度，此过程中金属棒产生热量Q＝5.8 J，不计导轨电阻及一切摩擦，取g＝10 m/s².求：

(1)金属棒达到的稳定速度是多大？

(2)金属棒从静止至达到稳定速度时所需的时间多长？

解析：(1)金属棒沿斜面上升到稳定速度时，设所受的安培力为F_A

由平衡条件得F＝mgsinθ+F_A

而F_A＝BIL＝BL

F＝

联立以上三式解得：v＝2 m/s

(2)由能量转化和守恒定律可得

Pt＝mgsinθ·s+mv²+Q

代入数据解得：t＝1.5 s.

答案：(1)2 m/s　(2)1.5 s

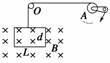
图38

10．(2009年开封模拟)如图36所示，一边长为a，电阻为R的等边三角形线框在外力作用下以速度v₀匀速穿过宽度均为a的两个匀强磁场区域，两磁场磁感应强度的大小均为B，方向相反，线框运动方向与底边平行且与磁场边缘垂直．以逆时针方向为电流正方向，从图示位置开始线框中感应电流I与沿运动方向的位移s的关系图象为(　)

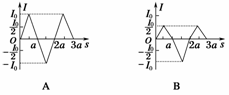
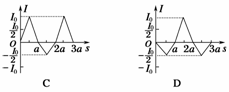
解析：线框的运动可分为三个阶段：进入Ⅰ磁场、离开Ⅰ磁场进入Ⅱ磁场和离开Ⅱ磁场．

进入Ⅰ磁场区时，开始时电流均匀增大，当有一半面积进入时电流达到最大，I1= ，然后又均匀减小，直到完全进入Ⅰ区．离开Ⅰ区，进入Ⅱ区时，在Ⅰ区和Ⅱ区内同时切割磁感线，电动势大小为两电动势之和，当有一半面积进入Ⅱ区时，电流达到最大值，I2=，然后又均匀减小，直到完全进入Ⅱ区，离开Ⅱ区时，电流大小的变化情况同进入Ⅰ区时一样，由于Ⅱ区磁场与Ⅰ区磁场反向，所以进入Ⅰ区与离开Ⅱ区时的电流同方向．

由上述分析可知，B项正确．

答案：B

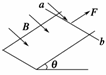
图37