
2.下列有机物命名正确的选项为( )
A.3,3-甲基丁烷 B.2,2-二甲基戊烷
C.2-甲基乙烷 D.2,3,3-三甲基丁烷
1.某烃的一种同分异构体只能生成一种氯代物,该烃的分子式可能是( )
A. B.
B. C.
C. D.
D.
20.(浙江省09年高考省教研室第一次抽样测试数学试题(理))已知函数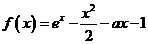 ,其中
,其中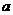 为实数.(1)若
为实数.(1)若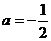 时,求曲线
时,求曲线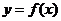 在点
在点 处的切线方程;(2)当
处的切线方程;(2)当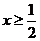 时,若关于
时,若关于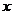 的不等式
的不等式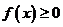 恒成立,试求
恒成立,试求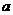 的取值范围.
的取值范围.
解析:(1).当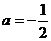 时,
时,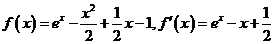 ,从而得
,从而得 ,故曲线
,故曲线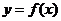 在点
在点 处的切线方程为
处的切线方程为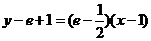 ,即
,即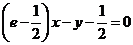 .
.
(2).由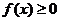 ,得
,得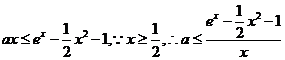 ,令
,令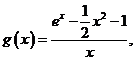 则
则 令
令 则
则 ,即
,即 在
在 上单调递增.所以
上单调递增.所以
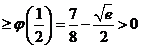 ,因此
,因此 ,故
,故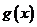 在
在 单调递增.则
单调递增.则 ,因此
,因此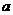 的取值范围是
的取值范围是 .
.
19.(温州市十校2008学年高三第一学期期初联考
数学试题(文))设函数 的图象关于原点对称,
的图象关于原点对称,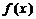 的图象在点
的图象在点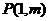 处的切线的斜率为
处的切线的斜率为 ,且当
,且当 时
时 有极值.
有极值.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的所有极值.
的所有极值.
解:(1) 由题意得b=d=0 (3分)
 ∴
∴
又∵ ∴
∴ 

即 , b=0,
, b=0,  , d=0
(7分)
, d=0
(7分)
(2)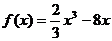
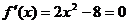 ∴
∴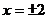 (9分)
(9分)
当x<-2时,

当-2<x<2时,

当x>2时,  (12分)
(12分)
∴ 的极值为
的极值为
 (14分)
(14分)
18.(温州十校2008学年度第一学期期中考试高三数学试题(文))(15分)已知函数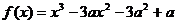
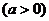
(1)求函数 的单调区间;
的单调区间;
(2)曲线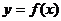 在点
在点 和
和
 处的切线都与
处的切线都与 轴垂直,若曲线
轴垂直,若曲线 在区间
在区间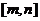 上与
上与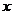 轴相交,求实数
轴相交,求实数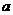 的取值范围;
的取值范围;
解:(1) ; …………3分
; …………3分
令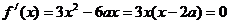 解得:
解得: ,
,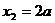
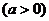 …………5分
…………5分
列出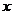 、
、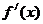 、
、 的变化值表
…………7分
的变化值表
…………7分
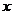 |
 |
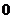 |
 |
 |
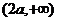 |
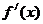 |
 |
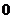 |
- |
0 |
 |
 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
由表可知:函数 的单调增区间:
的单调增区间: ,
,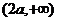 ;单调减区间
;单调减区间 ; …8分
; …8分
(2)由(1)可知,只有 ,
,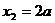 处切线都恰好与
处切线都恰好与 轴垂直;
轴垂直;
∴ ,
, ,
, …………11分
…………11分
由曲线 在区间
在区间 上与
上与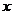 轴相交,可得:
轴相交,可得: ……13分
……13分
因为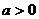 ,∴
,∴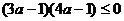 ,解得:
,解得: ;
;
故实数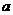 的取值范围是
的取值范围是 ;
…………15分
;
…………15分
17. (温州十校2008学年度第一学期期中高三数学试题(理))(本小题满分15分)
(温州十校2008学年度第一学期期中高三数学试题(理))(本小题满分15分)
如图,已知二次函数 ,直线
,直线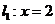 ,直线
,直线
 (其中
(其中 ,
,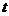 为常数);.若直线
为常数);.若直线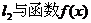 的图象以及
的图象以及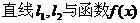 的图象所围成的封闭图形如阴影所示.
的图象所围成的封闭图形如阴影所示.
(Ⅰ)求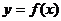 ;
(第17题图)
;
(第17题图)
(Ⅱ)求阴影面积s关于t的函数 的解析式;
的解析式;
(Ⅲ)若过点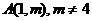 可作曲线
可作曲线 的三条切线,求实数m的取值范围.
的三条切线,求实数m的取值范围.
解:(I)由图可知二次函数的图象过点(0,0),(1,0)
则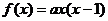 ,又因为图象过点(2,6)∴6=2a ∴a=3
,又因为图象过点(2,6)∴6=2a ∴a=3
∴函数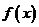 的解析式为
的解析式为 ………3分
………3分
(Ⅱ)由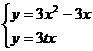 得
得
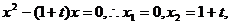
∵ ,∴直线
,∴直线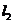 与
与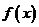 的图象的交点横坐标分别为0,1+t ,
的图象的交点横坐标分别为0,1+t ,
……………5分
由定积分的几何意义知:
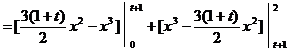
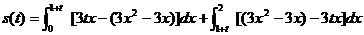
 ,
,  ……………8分
……………8分
(III)∵曲线方程为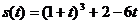 ,
,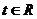 ,∴
,∴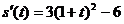 ,
,
∴点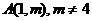 不在曲线上。设切点为
不在曲线上。设切点为 ,则点M的坐标满足
,则点M的坐标满足
 ,因
,因 ,故切线的斜率为
,故切线的斜率为
 ,整理得
,整理得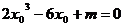 .
.
∵过点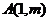 可作曲线的三条切线,
可作曲线的三条切线,
∴关于x0方程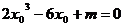 有三个实根.
……………12分
有三个实根.
……………12分
设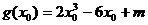 ,则
,则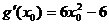 ,由
,由 得
得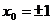
∵当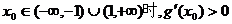 ∴
∴ 在
在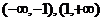 上单调递增,
上单调递增,
∵当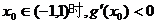 ,∴
,∴ 在
在 上单调递减.
上单调递减.
∴函数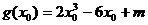 的极值点为
的极值点为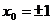 ,
,
∴关于x0方程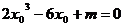 有三个实根的充要条件是
有三个实根的充要条件是 ,
,
解得 ,故所求的实数m的取值范围是
,故所求的实数m的取值范围是 。 ………15分
。 ………15分
16.((温州十校2008学年度第一学期期中高三数学试题(理))本小题满分14分)
已知函数 ,
,
(1)求函数 的单调区间;
的单调区间;
(2)若
 为大于0的常数),求
为大于0的常数),求 的最大值.
的最大值.
解:(1)由 ,可知
,可知
 ,
……………3分
,
……………3分
由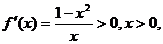 得
得
由 得
得 ……………6分
……………6分
∴函数 的单调递增区间为
的单调递增区间为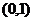 ;单调递减区间为
;单调递减区间为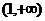 . ……………8分
. ……………8分
(2)①当 时,
时,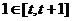 ,∴
,∴ .……………11分
.……………11分
②当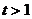 时,
时, 为减函数,
为减函数,
∴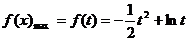 . …………………14分
. …………………14分
15.(2008学年第一学期期中杭州七校高三联考数学试题)(本题15分)
某公司有价值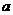 万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值
万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值 万元与技术改造投入
万元与技术改造投入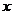 万元之间的关系满足:①
万元之间的关系满足:① 与
与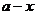 和
和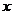 的乘积成正比;②
的乘积成正比;②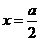 时,
时, ;③
;③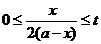 ,其中
,其中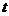 为常数,且
为常数,且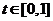 。
。
(1)设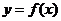 ,求
,求 表达式,并求
表达式,并求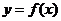 的定义域;
的定义域;
(2)求出附加值 的最大值,并求出此时的技术改造投入。
的最大值,并求出此时的技术改造投入。
解:(1)设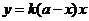 ,当
,当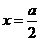 时,
时, ,可得:
,可得: ,∴
,∴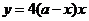
∴定义域为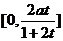 ,
,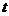 为常数,且
为常数,且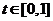 。 ………………7分
。 ………………7分
(2)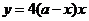

当 时,即
时,即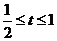 ,
,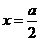 时,
时,
当 ,即
,即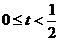 ,
,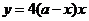 在
在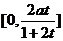 上为增函数
上为增函数
∴当 时,
时,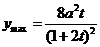 ……………………14分
……………………14分
∴当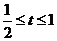 ,投入
,投入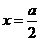 时,附加值y最大,为
时,附加值y最大,为 万元;
万元;
当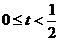 ,投入
,投入 时,附加值y最大,为
时,附加值y最大,为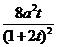 万元 ………15分
万元 ………15分
14.(绍兴市2008学年第一学期统考数学试题)★★已知函数 (1)判断函数
(1)判断函数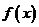 的对称性和奇偶性;(2)当
的对称性和奇偶性;(2)当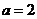 时,求使
时,求使 成立的
成立的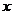 的集合;(3)若
的集合;(3)若 ,记
,记 ,且
,且 在
在 有最大值,求
有最大值,求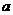 的取值范围.
的取值范围.
解析:(1)由函数 可知,函数
可知,函数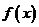 的图象关于直线
的图象关于直线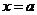 对称;
对称;
当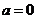 时,函数
时,函数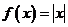 是一个偶函数;当
是一个偶函数;当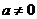 时,取特值:
时,取特值: ,故函数
,故函数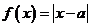 是非奇非偶函数.
是非奇非偶函数.
(2)由题意得 ,得
,得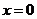 或
或 ;因此得
;因此得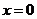 或
或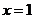 或
或 ,故所求的集合为
,故所求的集合为 .
.
(3)对于 ,
,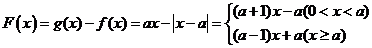
若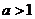 ,
, 在区间
在区间 上递增,无最大值;
上递增,无最大值;
若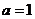 ,
,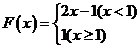 有最大值1
有最大值1
若 ,
, 在区间
在区间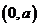 上递增,在
上递增,在 上递减,
上递减, 有最大值
有最大值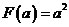 ;
;
综上所述得,当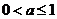 时,
时, 有最大值.
有最大值.
13.(2008-2009学年上学期期中高三数学试题(文))( 16分)已知二次函数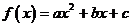 .
.
(1)若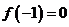 ,试判断函数
,试判断函数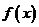 零点个数;
零点个数;
(2)若对 且
且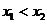 ,
,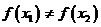 ,试证明
,试证明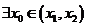 ,使
,使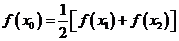 成立。
成立。
(3)是否存在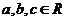 ,使
,使 同时满足以下条件①对
同时满足以下条件①对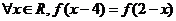 ,且
,且 ;②对
;②对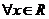 ,都有
,都有 。若存在,求出
。若存在,求出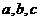 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
解:(1)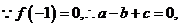
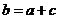
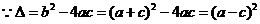 当
当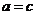 时
时 ,
,
函数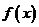 有一个零点;当
有一个零点;当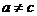 时,
时,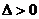 ,函数
,函数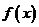 有两个零点。………4分
有两个零点。………4分
(2)令 ,则
,则

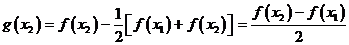 ,
,


在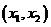 内必有一个实根。即
内必有一个实根。即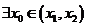 ,使
,使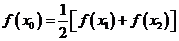 成立。
成立。
………………10分
(3)假设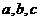 存在,由①知抛物线的对称轴为x=-1,且
存在,由①知抛物线的对称轴为x=-1,且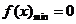
∴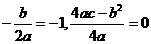
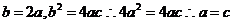
由②知对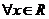 ,都有
,都有
令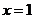 得
得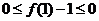
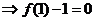
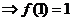
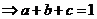 ……………13分
……………13分
由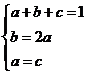 得
得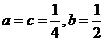 , ………………………………………………15分
, ………………………………………………15分
当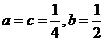 时,
时,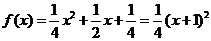 ,其顶点为(-1,0)满足条件①,又
,其顶点为(-1,0)满足条件①,又
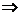 对
对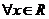 ,都有
,都有 ,满足条件②。∴存在
,满足条件②。∴存在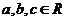 ,使
,使 同时满足条件①、②。…………………………16分
同时满足条件①、②。…………………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com