1．祈盼“五谷丰登”、“六畜兴旺”是我国古代劳动人民的美好愿望。这反映了中国古代农业经济的哪一特点

A.古代人们有家畜养殖的传统　　　　　　　 B.种植业为主，家畜饲养业为辅

C.牛耕完善了精耕细作生产模式　　　　　　 D.采用“男耕女织”式的经营方式

13．(20分)已知函数f(x)＝x+log₃.

(1)求f(x)+f(4－x)的值；

(2)猜想函数f(x)的图象具有怎样的对称性，并给出证明．

解：(1)f(x)+f(4－x)＝x+log₃+4－x+

log₃＝4+log₃+log₃＝4.

(2)关于点P(2,2)对称．

证明：设Q(x，y)为函数f(x)＝x+log₃图象上的任一点，若点Q关于点P的对称点为Q₁(x₁，y₁)，

则⇒

f(x₁)＝x₁+log₃＝4－x+log₃＝4－x－

log₃＝4－y＝y₁，∴函数y＝f(x)的图象关于点P(2,2)对称．

12．(15分)(2009·山东潍坊二模)已知函数f(x)＝log₂(x+1)，将y＝f(x)的图象向左平移1个单位，再将图象上所有点

的纵坐标伸长到原来的2倍，横坐标不变，得到函数y＝g(x)的图象．

(1)求y＝g(x)的解析式及定义域；

(2)求函数F(x)＝f(x－1)－g(x)的最大值．

解：(1)f(x)＝log₂(x+1)y＝log₂(x+2)纵坐标伸长到原来的2倍y＝2log₂(x+2)，即g(x)＝2log₂(x+2)，∵x+2>0.

∴x>－2.∴定义域为(－2，+∞)．

(2)∵F(x)＝f(x－1)－g(x)＝log₂x－2log₂(x+2)＝log₂(x>0)＝log₂＝log₂≤log₂＝－3，

∴当x＝2时，F(x)_max＝－3.

11．(15分)分别画出下列函数的图象：

(1)y＝|lgx|；(2)y＝2^x+2；(3)y＝x²－2|x|－1.

解：(1)y＝　　　 　　　　　　　　　　　　　　

(2)将y＝2^x的图象向左平移2个单位．

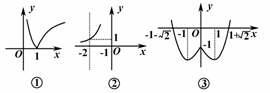
图6

(3)y＝

10．若函数f(x)＝log₂|ax－1|的图象的对称轴为x＝2，则非零实数a的值是__________．

解析：∵函数f(x)的图象的对称轴为x＝2，∴f(2+x)＝f(2－x)，即|a(2－x)－1|＝|a(2+x)－1|，∵a≠0，∴2a－1＝0，∴a＝.

答案：

9．已知f(x)是定义域为(－∞，0)∪(0，+∞)上的奇函数，在区间(0，+∞)上单调递增，当x>0时，f(x)的图象如图5所示：若x·[f(x)－f(－x)]<0，则x的取值范围是__________．

解析：∵f(x)为奇函数，

∴x·[f(x)－f(－x)]＝2x·f(x)<0.

又f(x)在定义域上的图象如题图，

∴取值范围为(－3,0)∪(0,3)．

答案：(－3,0)∪(0,3)

8．已知最小正周期为2的函数y＝f(x)，当x∈[－1,1]时，f(x)＝x²，则函数y＝f(x)(x∈R)的图象与y＝|log₅x|的图象的交点个数为__________．

解析：由图4可知有5个交点．

图4

答案：5个

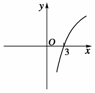
图5

7．如果函数y＝f(x)满足f(x)＝f(2－x)，那么函数y＝f(x)的图象关于直线x＝__________对称．

解析：f(x)＝f(2－x)⇔f[1－(1－x)]＝f[1+(1－x)]⇔f(1－x)＝f(1+x)．∴函数y＝f(x)的图象关于直线x＝1对称．

答案：1

6．(2009·湖南高考)如图3，当参数λ＝λ₁，λ₂时，连续函数y＝

(x≥0)的图像分别对应曲线C₁和C₂，则　　　　　　　　　　　　　　　　　 　(　)

A．0<λ₁<λ₂　　　　　　　　　　　　　　　　　　　　　　　　　 B．0<λ₂<λ₁

C．λ₁<λ₂<0　　　　　　　　　　　　　　　　　　　　　　 D．λ₂<λ₁<0

解析：如果λ<0，定义域不可能为[0，+∞)，排除C、D.

又∵C₂的图象在C₁的图象的上方，

∴>⇒<⇒λ₂<λ₁.故选B.

答案：B

5．(2009·安徽高考)设a<b，函数y＝(x－a)²(x－b)的图像可能是　　　　　　　　　　　 (　)

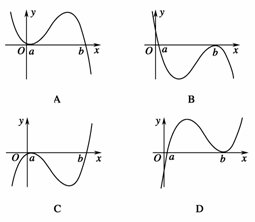
解析：当x>b时，y>0，由数轴穿根法可知，从右上向左下穿，奇次穿偶次不穿可知，只有C正确．

答案：C

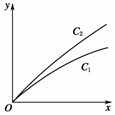
图3