
3.动量定理的定量计算
利用动量定理解题,必须按照以下几个步骤进行:
(1)明确研究对象和研究过程。研究对象可以是一个物体,也可以是几个物体组成的质点组。质点组内各物体可以是保持相对静止的,也可以是相对运动的。研究过程既可以是全过程,也可以是全过程中的某一阶段。
(2)进行受力分析。只分析研究对象以外的物体施给研究对象的力。所有外力之和为合外力。研究对象内部的相互作用力(内力)会改变系统内某一物体的动量,但不影响系统的总动量,因此不必分析内力。如果在所选定的研究过程中的不同阶段中物体的受力情况不同,就要分别计算它们的冲量,然后求它们的矢量和。
(3)规定正方向。由于力、冲量、速度、动量都是矢量,在一维的情况下,列式前要先规定一个正方向,和这个方向一致的矢量为正,反之为负。
(4)写出研究对象的初、末动量和合外力的冲量(或各外力在各个阶段的冲量的矢量和)。
(5)根据动量定理列式求解。
[例7]质量为m的小球,从沙坑上方自由下落,经过时间t1到达沙坑表面,又经过时间t2停在沙坑里。求:
(1)沙对小球的平均阻力F;
(2)小球在沙坑里下落过程所受的总冲量I。
 解析:设刚开始下落的位置为A,刚好接触沙的位置为B,在沙中到达的最低点为C。
解析:设刚开始下落的位置为A,刚好接触沙的位置为B,在沙中到达的最低点为C。
(1)在下落的全过程对小球用动量定理:重力作用时间为t1+t2,而阻力作用时间仅为t2,以竖直向下为正方向,有:
mg(t1+t2)-Ft2=0, 解得: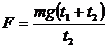
(2)仍然在下落的全过程对小球用动量定理:在t1时间内只有重力的冲量,在t2时间内只有总冲量(已包括重力冲量在内),以竖直向下为正方向,有:
mgt1-I=0,∴I=mgt1
点评:这种题本身并不难,也不复杂,但一定要认真审题。要根据题意所要求的冲量将各个外力灵活组合。若本题目给出小球自由下落的高度,可先把高度转换成时间后再用动量定理。当t1>> t2时,F>>mg。
 [例8] 质量为M的汽车带着质量为m的拖车在平直公路上以加速度a匀加速前进,当速度为v0时拖车突然与汽车脱钩,到拖车停下瞬间司机才发现。若汽车的牵引力一直未变,车与路面的动摩擦因数为μ,那么拖车刚停下时,汽车的瞬时速度是多大?
[例8] 质量为M的汽车带着质量为m的拖车在平直公路上以加速度a匀加速前进,当速度为v0时拖车突然与汽车脱钩,到拖车停下瞬间司机才发现。若汽车的牵引力一直未变,车与路面的动摩擦因数为μ,那么拖车刚停下时,汽车的瞬时速度是多大?
解析:以汽车和拖车系统为研究对象,全过程系统受的合外力始终为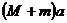 ,该过程经历时间为v0/μg,末状态拖车的动量为零。全过程对系统用动量定理可得:
,该过程经历时间为v0/μg,末状态拖车的动量为零。全过程对系统用动量定理可得:
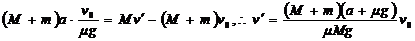
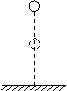 点评:这种方法只能用在拖车停下之前。因为拖车停下后,系统受的合外力中少了拖车受到的摩擦力,因此合外力大小不再是
点评:这种方法只能用在拖车停下之前。因为拖车停下后,系统受的合外力中少了拖车受到的摩擦力,因此合外力大小不再是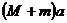 。
。
[例9] 质量为m=1kg的小球由高h1=0.45m处自由下落,落到水平地面后,反跳的最大高度为h2=0.2m,从小球下落到反跳到最高点经历的时间为Δt=0.6s,取g=10m/s2。求:小球撞击地面过程中,球对地面的平均压力的大小F。
解析:以小球为研究对象,从开始下落到反跳到最高点的全过程动量变化为零,根据下降、上升高度可知其中下落、上升分别用时t1=0.3s和t2=0.2s,因此与地面作用的时间必为t3=0.1s。由动量定理得:mgΔt-Ft3=0 ,F=60N
[例10] 一个质量为m=2kg的物体,在F1=8N的水平推力作用下,从静止开始沿水平面运动了t1=5s,然后推力减小为F2=5N,方向不变,物体又运动了t2=4s后撤去外力,物体再经 过t3=6s停下来。试求物体在水平面上所受的摩擦力。
解析:
解法l 取物体为研究对象,它的运动可明显分为三个过程。设第一、二两过程末的速度分别为v1和v2。,物体所受摩擦力为f,规定推力的方向为正方向。根据动量定理对三个过程分别有:
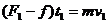
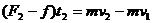
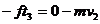
联立上述三式得 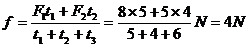
解法2 规定推力的方向为正方向,在物体运动的整个过程中,物体的初动量p1=0,末动量p2=0。据动量定理有
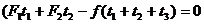
即: 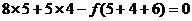
解得 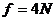
点评:遇到涉及力、时间和速度变化的问题时,运用动量定理解答往往比运用牛顿运动定律及运动学规律求解简便。由解法2可知,合理选取研究过程,能简化解题步骤,提高解题速度。本题也可以用牛顿运动定律求解。
2.动量定理的定性应用
[例4] 鸡蛋从同一高度自由下落,第一次落在地板上,鸡蛋被打破;第二次落在泡沫塑料垫上,没有被打破。这是为什么?
解析:两次碰地(或碰塑料垫)瞬间鸡蛋的初速度相同,而末速度都是零也相同,所以两次碰撞过程鸡蛋的动量变化相同。根据Ft=Δp,第一次与地板作用时的接触时间短,作用力大,所以鸡蛋被打破;第二次与泡沫塑料垫作用的接触时间长,作用力小,所以鸡蛋没有被打破。(再说得准确一点应该指出:鸡蛋被打破是因为受到的压强大。鸡蛋和地板相互作用时的接触面积小而作用力大,所以压强大,鸡蛋被打破;鸡蛋和泡沫塑料垫相互作用时的接触面积大而作用力小,所以压强小,鸡蛋未被打破。)
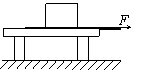 [例5]某同学要把压在木块下的纸抽出来。第一次他将纸迅速抽出,木块几乎不动;第二次他将纸较慢地抽出,木块反而被拉动了。这是为什么?
[例5]某同学要把压在木块下的纸抽出来。第一次他将纸迅速抽出,木块几乎不动;第二次他将纸较慢地抽出,木块反而被拉动了。这是为什么?
解析:物体动量的改变不是取决于合力的大小,而是取决于合力冲量的大小。在水平方向上,第一次木块受到的是滑动摩擦力,一般来说大于第二次受到的静摩擦力;但第一次力的作用时间极短,摩擦力的冲量小,因此木块没有明显的动量变化,几乎不动。第二次摩擦力虽然较小,但它的作用时间长,摩擦力的冲量反而大,因此木块会有明显的动量变化。
[例6] 一粒钢珠从静止状态开始自由下落,然后陷人泥潭中。若把在空中下落的过程称为过程Ⅰ,进人泥潭直到停止的过程称为过程Ⅱ, 则( )
A、过程I中钢珠的动量的改变量等于重力的冲量
B、过程Ⅱ中阻力的冲量的大小等于过程I中重力的冲量的大小
C、I、Ⅱ两个过程中合外力的总冲量等于零
D、过程Ⅱ中钢珠的动量的改变量等于零
解析:根据动量定理可知,在过程I中,钢珠从静止状态自由下落.不计空气阻力,小球所受的合外力即为重力,因此钢珠的动量的改变量等于重力的 冲量,选项A正确;过程I中阻力的冲量的大小等于过程I中重力的冲量的大小与过程Ⅱ中重力的冲量的大小之和,显然B选项不对;在I、Ⅱ两个过程中,钢珠动量的改变量各不为零.且它们大小相等、方向相反,但从整体看,钢珠动量的改变量为零,故合外力的总冲量等于零,故C选项正确,D选项错误。因此,本题的正确选项为A、C。
1.动量定理
物体所受合外力的冲量等于物体的动量变化。既I=Δp
(1)动量定理表明冲量是使物体动量发生变化的原因,冲量是物体动量变化的量度。这里所说的冲量必须是物体所受的合外力的冲量(或者说是物体所受各外力冲量的矢量和)。
(2)动量定理给出了冲量(过程量)和动量变化(状态量)间的互求关系。
(3)现代物理学把力定义为物体动量的变化率: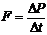 (牛顿第二定律的动量形式)。
(牛顿第二定律的动量形式)。
(4)动量定理的表达式是矢量式。在一维的情况下,各个矢量必须以同一个规定的方向为正。
点评:要注意区分“合外力的冲量”和“某个力的冲量”,根据动量定理,是“合外力的冲量”等于动量的变化量,而不是“某个力的冲量” 等于动量的变化量。这是在应用动量定理解题时经常出错的地方,要引起注意。
[例3]以初速度v0平抛出一个质量为m的物体,抛出后t秒内物体的动量变化是多少?
解析:因为合外力就是重力,所以Δp=Ft=mgt
点评:有了动量定理,不论是求合力的冲量还是求物体动量的变化,都有了两种可供选择的等价的方法。本题用冲量求解,比先求末动量,再求初、末动量的矢量差要方便得多。当合外力为恒力时往往用Ft来求较为简单;当合外力为变力时,在高中阶段只能用Δp来求。
2.冲量
按定义,力和力的作用时间的乘积叫做冲量:I=Ft
(1)冲量是描述力的时间积累效应的物理量,是过程量,它与时间相对应。
(2)冲量是矢量,它的方向由力的方向决定(不能说和力的方向相同)。如果力的方向在作用时间内保持不变,那么冲量的方向就和力的方向相同。如果力的方向在不断变化,如绳子拉物体做圆周运动,则绳的拉力在时间t内的冲量,就不能说是力的方向就是冲量的方向。对于方向不断变化的力的冲量,其方向可以通过动量变化的方向间接得出。
(3)高中阶段只要求会用I=Ft计算恒力的冲量。对于变力的冲量,高中阶段只能利用动量定理通过物体的动量变化来求。
(4)要注意的是:冲量和功不同。恒力在一段时间内可能不作功,但一定有冲量。
 [例2] 质量为m的小球由高为H的光滑固定斜面顶端无初速滑到底端过程中,重力、弹力、合力的冲量各是多大?
[例2] 质量为m的小球由高为H的光滑固定斜面顶端无初速滑到底端过程中,重力、弹力、合力的冲量各是多大?
解析:力的作用时间都是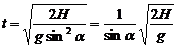 ,力的大小依次是mg、mgcosα和mgsinα,所以它们的冲量依次是:
,力的大小依次是mg、mgcosα和mgsinα,所以它们的冲量依次是: 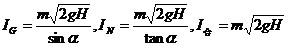
点评:特别要注意,该过程中弹力虽然不做功,但对物体有冲量。
2.动量的变化:
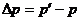
由于动量为矢量,则求解动量的变化时,其运算遵循平行四边形定则。
(1)若初末动量在同一直线上,则在选定正方向的前提下,可化矢量运算为代数运算。
(2)若初末动量不在同一直线上,则运算遵循平行四边形定则。
[例1]一个质量为m=40g的乒乓球自高处落下,以速度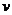 =1m/s碰地,竖直向上弹回,碰撞时间极短,离地的速率为
=1m/s碰地,竖直向上弹回,碰撞时间极短,离地的速率为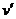 =0.5m/s。求在碰撞过程中,乒乓球动量变化为多少?
=0.5m/s。求在碰撞过程中,乒乓球动量变化为多少?
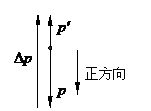 解析:取竖直向下为正方向,乒乓球的初动量为:
解析:取竖直向下为正方向,乒乓球的初动量为:
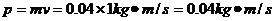
乒乓球的末动量为:
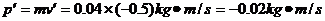
乒乓球动量的变化为:
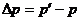 =
=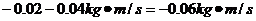
负号表示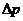 的方向与所取的正方向相反,即竖直向上。
的方向与所取的正方向相反,即竖直向上。
1.动量
按定义,物体的质量和速度的乘积叫做动量:p=mv
(1)动量是描述物体运动状态的一个状态量,它与时刻相对应。
(2)动量是矢量,它的方向和速度的方向相同。
(3)动量的相对性:由于物体的速度与参考系的选取有关,所以物体的动量也与参考系选取有关,因而动量具有相对性。题中没有特别说明的,一般取地面或相对地面静止的物体为参考系。
9.(2004年全国理综第23题,16分)在勇气号火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0,求它第二次落到火星表面时速度的大小,计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r,周期为T。火星可视为半径为r0的均匀球体。
8.我国自制新型“长征”运载火箭,将模拟载人航天试验飞船“神舟三号”送入预定轨道,飞船绕地球遨游太空t=7天后又顺利返回地面.飞船在运动过程中进行了预定的空间科学实验,获得圆满成功。
(1)设飞船轨道离地高度为h,地球半径为R,地面重力加速度为g.则“神舟三号”飞船绕地球正常运转多少圈?(用给定字母表示).
(2)若h=600 km,R=6400 km,则圈数为多少?
7.(1998年全国卷)宇航员站在某一星球表面上的某高处,沿水平方向抛出一小球。经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到2倍,则抛出点与落地点之间的距离为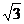 L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
L。已知两落地点在同一水平面上,该星球的半径为R,万有引力常数为G。求该星球的质量M。
6.航天技术的不断发展,为人类探索宇宙创造了条件.1998年1月发射的“月球勘探者号”空间探测器,运用最新科技手段对月球进行近距离勘探,在月球重力分布、磁场分布及元素测定等方面取得最新成果.探测器在一些环形山中央发现了质量密集区,当飞越这些重力异常区域时
A.探测器受到的月球对它的万有引力将变大
B.探测器运行的轨道半径将变大
C.探测器飞行的速率将变大
D.探测器飞行的速率将变小
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com