2.阿伏伽德罗常数N_A= 6.0×10²³ mol^－-1，分子直径的数量级d= 　1.0×10^-10m　　　　　 。

1．分子运动论基本内容是：

(1) 物质是由分子组成的　　　　　　 ；

(2) 组成物质的分子在不停地做无规则的运动　 ；

(3)　 分子间存在相互作用力　　　　　　　　 。

4.分子间的的相互作用力。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

3.分子的热运动、布朗运动。

2.阿伏伽德罗常数。

1.物质是由大量分子组成的。

9.设计实验举例

例11 利用手头的常用仪器，粗略测定玩具手枪子弹射出时的初速度。除玩具手枪外，所给的测量仪器为：⑴只有秒表；⑵只有米尺。

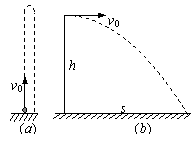
解：

(1)若只有秒表，可如图(a)，将玩具手枪从地面竖直向上发射子 弹，用秒表记下从发射到子弹落会地面所用的时间t，则子弹上升的时间为t/2，故子弹初速度v₀=gt/2。

　　 (2)若只有米尺，可如图(b)，将玩具手枪子弹从某一高度处水平射出，用米尺测量射出时离地面的高度h和水平射程s，则子弹初速度。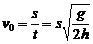

例12 某同学在做探究弹力和弹簧伸长的关系的实验中，设计了如图所示的实验装置。所用的钩码每只的质量都是30g，他先测出不挂钩码时弹簧的自然长度，再将5个钩码逐个挂在弹簧的下端，每次都测出相应的弹簧总长度，将数据填在了下面的表中。(弹力始终未超过弹性限度，取g=9.8m/s²)

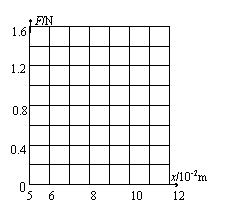
(1)试根据这些实验数据在右图给定的坐标纸上作出弹簧所受弹力大小F跟弹簧总长L之间的函数关系图线，说明图线跟坐标轴交点的物理意义。

(2)上一问所得图线的物理意义是什么?该弹簧的劲度k是多大?

解：

(1)根据实验数据在坐标纸上描出的点，基本上在同一条直线 　上。可以判定F和L间是一次函数关系。画一条直线，使尽可能多的点落在这条直线上，不在直线上的点均匀地分布在直线两侧。该图线跟横轴交点的横坐标表示弹簧的原长。

(2)图线的物理意义是表明弹簧的弹力大小和弹簧伸长量大小成正比。由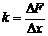可得k=25N/m。

8.用单摆测定重力加速度

(1)摆长的测量：让单摆自由下垂，用米尺量出摆线长L^/(读到0.1mm)，用游标卡尺量出摆球直径(读到0. 1mm)算出半径r，则摆长L=L^/+r

(2)开始摆动时需注意：摆角要小于5°(要保证做简谐运动，不要使摆动成为圆锥摆)

(3)从摆球通过最低点时开始计时，测出单摆做50次全振动所用的时间，算出周期的平均值T。

(4)改变摆长重做几次实验，计算每次实验得到的重力加速度，再求这些重力加速度的平均值。

例9一组同学在做“用单摆测定重力加速度”的实验中，用正确的操作方法，测定了6组摆长L和周期T的对应值。为了求出当地的重力加速度g，4位同学提出了4种不同的方法：①从测定的6组数据中任意选取1组，用公式g=4π²L/T ²求出g作为测量值；②分别求出6个L值的平均值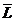和6个T值的平均值，用公式g=4π²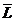/²求出g作为测量值；③分别用6组L、T的对应值，用公式g=4π²L/T ²求出6个对应的g值，再求这6个g的平均值作为测量值；④在坐标纸上作出T ²-L图象，从图象中计算出图线的斜率K，根据g=4π²/K求出g作为测量值。

　　 你认为以上4种方法中，错误的是哪一种____(填代号即可)，其余正确方法中偶然误差最小的是哪一种______(填代号即可)。

解：错误的是②，因为L和T之间不是一次函数的关系。偶然误差最小的是④，因为偶然误差总是有时偏大有时偏小。而描点后画线时要求尽可能多的点在该直线上，其余点尽可能均衡地分布在该直线两侧，实际上是把偶然误差减小到最小了。

例10某同学在家里做用单摆测定重力加速度的实验，但没有合适的摆球，他找到了一块大小为3cm左右，外形不规则的大理石块代替小球。他设计的实验步骤是：

　 A.将石块用细尼龙线系好，结点为M，将尼龙线的上端固定于O点

　 B.用刻度尺测量OM间尼龙线的长度L作为摆长

　 C.将石块拉开一个大约α=30°的角度,然后由静止释放

　 D.从摆球摆到最高点时开始计时，测出30次全振动的总时间t,，由T=t/30得出周期

　 E.改变OM间尼龙线的长度再做几次实验，记下相应的L和T

　 F.求出多次实验中测得的的平均值作为计算时使用的数据,带入公式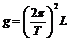求出重力加速度g

　　 ⑴你认为该同学以上实验步骤中有重大错误的是_______________。为什么?

　　 ⑵该同学用OM的长作为摆长，这样做引起的系统误差将使重力加速度的测量值比真实值偏大还是偏小?________。你认为用什么方法可以解决摆长无法准确测量的困难?

解：

(1)B(摆长应从悬点到大理石块的质心)、C(摆角太大，不能看作简谐运动)、F(必须先分别求和各组L和T值对应的g，再取所求得的各个g的平均值)。

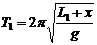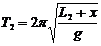(2)小。设两次实验中摆线长分别为L₁、L₂，对应的周期分别为T₁、T₂，石块质心到M点的距离为x，由和可解得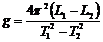

7.验证机械能守恒定律

本实验要求验证自由下落过程中机械能守恒，图示纸带的左端是用夹子夹重物的一端。

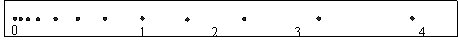
(1)要多做几次实验，选点迹清楚，且第一、二两点间距离接近2mm的纸带进行测量。

(2)用刻度尺量出从0点到1、2、3、4、5各点的距离h₁、h₂、h₃、h₄、h₅，利用“匀变速直线运动中间时刻的即时速度等于该段位移内的平均速度”，算出2、3、4各点对应的即时速度v₂、v₃、v₄，验证与2、3、4各点对应的重力势能减少量mgh和动能增加量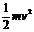是否相等。

(3)由于摩擦和空气阻力的影响，本实验的系统误差总是使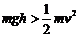

(4)本实验不需要在打下的点中取计数点。也不需要测重物的质量。

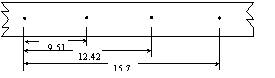例8在用落体法验证机械能守恒定律时，某同学按照正确的操作选得纸带如右。其中O是起始点，A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O到A、B、C各点的距离,并记录在图中(单位cm)。

(1)这三个数据中不符合有效数字读数要求的是_____ ,应记作_______cm。

(2)该同学用重锤在OB段的运动来验证机械能守恒，已知当地的重力加速度g=9.80m/s²，他用AC段的平均速度作为跟B点对应的物体的即时速度，则该段重锤重力势能的减少量为_______，而动能的增加量为________，(均保留3位有效数字，重锤质量用m表示).这样验证的系统误差总是使重力势能的减少量_______动能的增加量，原因是_________________。

(3)另一位同学根据同一条纸带，同一组数据，也用重锤在OB段的运动来验证机械能守恒，不过他数了一下：从打点计时器打下的第一个点O数起，图中的B是打点计时器打下的第9个点。因此他用v_B=gt计算跟B点对应的物体的即时速度，得到动能的增加量为______，这样验证时的系统误差总是使重力势能的减少量_______动能的增加量,原因是________________________________。

解： (1)OC，15.70

(2)1.22m，1.20m，大于，v是实际速度，因为有摩擦生热，减少的重力势能一部分转化为内能；

(3)1.23m，小于，v是按照自由落体计算的，对应的下落高度比实际测得的高度要大。

6.研究平抛物体的运动

(1)斜槽末端的切线必须水平。

(2)用重锤线检验坐标纸上的竖直线是否竖直。

(3)以斜槽末端所在的点为坐标原点。

(4)如果是用白纸，则应以斜槽末端所在的点为坐标原点，在斜槽末端悬挂重锤线，先以重锤线方向确定y轴方向，再用直角三角板画出水平线作为x轴，建立直角坐标系。

(5)每次小球应从斜槽上的同一位置由静止开始下滑。

(6)由描迹法得到小球平抛的轨迹，从轨迹上任何一点的横纵坐标都可以计算出该平抛物体抛出时的初速度。

(7)若用闪光照相来研究，所得到的照片上相邻小球间的时间间隔是相等的，利用这一 结论和运动分解的知识，可以求小球平抛的初速度，也可以求小球在任何一个位置的瞬时速度。

例7.如图所示，在“研究平抛物体的运动”的实验中，某同学按要求描绘出了小球做平抛运动过程中的三个点A、B、C，并利用刻度尺量出了三点的坐标依次是A(0.369，0.112)、B(0.630，0.327)、C(0.761，0.480)，单位为m 。又称得小球的质量为20g，试计算小球平抛的初动能E_K。

解：小球的初速度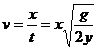，因此初动能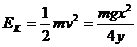，带入数据后得：E_K1=0.0596J，E_K2=0.0594J，E_K3=0.0591J，因此初动能的平均值为E_K=0.0594J