2. 下列实验中均需要的仪器是

① 配制一定物质的量浓度的溶液 ② PH试纸的使用 ③过滤 ④ 蒸发

A. 　试管　　 B.　 胶头滴管　　 C.　 玻璃棒　　　 D.　 漏斗

1. 下列常用实验仪器中，不能直接用于混合物的分离或提纯的是

A．分液漏斗　　 B．普通漏斗　　 C. 蒸馏烧瓶　　 D．容量瓶

2．在解决相似三角形时，一定要注意对应角和对应边，否则容易出错．

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

1．在应用平行截割定理时，一定要注意对应线段成比例．

12．如下图所示，四边形ABCD是平行四边形，点E在边BA的延长线上，CE交AD于点F，∠ECA＝∠D.

求证：AC·BE＝CE·AD.

[证明]　∵四边形ABCD是平行四边形，

∴AF∥BC.∴＝，

又∵AE∥CD，∴△AFE∽△DFC，

∴＝即＝＝，

又∵∠ECA＝∠D，∠CAF＝∠DAC，

∴△AFC∽△ACD，

∴＝，∴＝，∴AC·BE＝CE·AD.

亲爱的同学请你写上学习心得

11．如下图所示，在△ABC中，AB＝AC，AD是边BC的中线，P为AD上一点，CF∥AB，BP的延长线分别交AC，CF于点E，F，求证：BP²＝PE·PF.

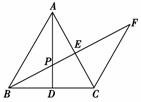
[分析]　要证明BP²＝PE·PF可以考虑将这三条线段(或与之相等的线段)组成两个相似三角形，这两个相似三角形应分别有一条边等于BP，考虑求证中涉及线段的位置关系，可取与BP相等的线段PC.

[证明]　连结PC，∵AB＝AC，∴中线AD是此等腰三角形的对称轴．

∴∠ABP＝∠ACP，PB＝PC，又∵CF∥AB，

∴∠CFP＝∠ABP＝∠PCE.

又∵∠CPF为两个三角形的公共角，

∴△CPE∽△FPC，

∴＝.

∴BP²＝PC²＝PE·PF.

10．如下图所示，在矩形ABCD中，AB＝12，AD＝10，将此矩形折叠，使点B落在AD边上的中点E处，则折痕FG的长为________．

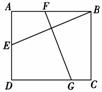
[解析]　依题意知，FG垂直平分线段BE，

过F作FH⊥CD，垂足为F.则∠ABE＝∠HFG，

∴Rt△ABE∽Rt△HFG，∴＝，∵AB＝12，AD＝10，∴BE＝13，∴FG＝＝＝.

[答案]　

9．在矩形ABCD中，AB＝a，BC＝b，M是BC的中点，DE⊥AM，E是垂足，则DE＝________.

[解析]　∵∠BAM+∠DAM＝∠DAM+∠ADE＝90°，

∴∠BAM＝∠ADE，∠ABM＝∠AED＝90°，

∴△ABM∽△DEA，

∴＝，DE＝×AB＝＝.

[答案]　

8．(2009·茂名模拟)如下图所示，在梯形ABCD中，AD∥BC，BD、AC相交于O，过O的直线分别交AB、CD于E、F，且EF∥BC，若AD＝12，BC＝20，则EF＝________.

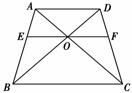
[解析]　△AOD∽△BOC，∴＝＝＝，又∵△BOE∽△BOA，∴＝，∴OE＝AD＝，同理可得OF＝，∴EF＝15.

[答案]　15

7．(2008·梅州一模)如图，在四边形ABCD中，EF∥BC，FG∥AD，则+＝________.

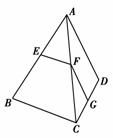
[答案]　1