
21、(1) 在氯化钡溶液中通入SO2气体,溶液仍澄清;若将BaCl2溶液分盛两支试管,一支加硝酸,另一支加烧碱溶液,然后再通入SO2气体,结果两支试管都有沉淀。由此得出下列结论合理的是 A、氯化钡有两性 B、两支试管的沉淀均是亚硫酸钡 C、SO2有还原性和酸性 D、升高PH值使SO2水溶液中SO32-浓度增大。 (2)下列试剂中,可以确定某无色混合气体中一定含有SO2和CO2的是 ①石灰水②品红溶液③溴水④KMnO4酸性溶液 A、④① B、③① C、①② D、②④①
(3)物质的量浓度相同、体积相同的下列溶液中,吸收SO2气体的量最多的是 A、NH3•H2O B、Na2CO3 C、Na2S D、Ba(OH)2
19、(1)向氯化铁和氯化钡的酸性混合溶液中通入SO2气体,有白色沉淀生成,此沉淀是 A、BaSO4 B、FeS C、BaSO3 D、S 解析:题中隐含的条件为:该白色沉淀不溶于酸,可以排除B、C。 由Fe3+有氧化性,SO2有还原性,两者要发生氧化还原反应,硫元素化合价升高,生成的SO42-与Ba2+结合成BaSO4。 答案:A 评析:根据该题隐含的信息,可写出下列化学方程式:2FeCl3+SO2+2H2O=2FeCl2+H2SO4+2HCl。 例20(1)导致下列现象的主要原因,与排放SO2有关的是: A、酸雨 B、光化学烟雾 C、臭氧空洞 D、温室效应 误答原因:错选C。把“主要原因”误认为“可能原因”。 解析:A酸雨形成的主要原因是大气中SO2的排放。 B光化学烟雾是指氮氧化物和碳氢化合物(HC)在大气环境中受强烈的太阳紫外线照射后产生一种新的二次污染物 C人工合成的一些含氯和含溴的物质是造成南极臭氧洞的元凶,最典型的是氟氯碳化合物(CFC,俗称氟里昂)和含溴化合物哈龙(Halon)。越来越多的科学证据证实,氯和溴在平流层通过催化化学过程破坏臭氧是造成南极臭氧洞的根本原因。 D温室效应主要是由于现代化工业社会过多燃烧煤炭、石油和天然气,大量排放尾气,这些燃料燃烧后放出大量的二氧化碳气体进入大气造成的。 答案:A (2)地球上大气层有一层臭氧层,保护地球上的生物免遭紫外线的伤害,臭氧层有很强的氧化性,下列能使臭氧层受到破坏的是 A、SO2 B、CO2 C、CO D、N2 提示:臭氧具有很强的氧化性,能与具有还原性的气体反应。 答案:AC
18、下列有关SO3的描述中不正确的是: A、在一定条件下分解为SO2和O2 B、是硫酸的酸酐 C、其中的硫元素已达最高价,不能再被氧化 D、取8gSO3溶于92g水中即得8%的溶液
误答原因:错选A。原因是没有认识到SO2的催化氧化为可逆反应。 正确分析:由于SO2的催化氧化是可逆反应,所以SO3在同样条件下也可分解生成SO2和O2,A正确。 BC的说法也正确。 SO3溶于水后与水发生反应生成H2SO4(SO3+H2O=H2SO4),所以SO3的水溶液中真正的溶质是H2SO4,质量显然大于8g,质量分数为9.9%,D错。 答案:D
17、用浓硫酸吸收三氧化硫可以得到H2SO4•SO3,若用1000g98%的硫酸充分吸收三氧化硫后,再进行稀释,可得到98%的硫酸的质量是多少千克?(要求详细过程)
用浓硫酸吸收三氧化硫可以得到H2SO4•SO3,若用1000g98%的硫酸充分吸收三氧化硫后,再进行稀释,可得到98%的硫酸的质量是多少千克?(要求详细过程) 错解:设最后可得98%的硫酸的质量为x H2SO4------ H2SO4•SO3------ 2H2SO4 98g 196g (1000×98%)g 98%x X=(1000×98%)g×196g/(98g×98%) =2000g =2kg 误答原因:未考虑原有98%H2SO4中的水可与三氧化硫生成硫酸继续吸收三氧化硫。 正确分析:解法一(分割考虑)、设98%硫酸中由溶质H2SO4吸收可得98%的硫酸的质量为x,由溶剂水吸收可得98%的硫酸的质量为y,则 H2SO4------ H2SO4•SO3------ 2H2SO4 98g 196g (1000×98%)g 98%x X=(1000×98%)g×196g/(98g×98%) =2000g =2kg H2O-------H2SO4•SO3------ 2H2SO4 18g 196g 1000×(1-98%)g 98%y y=1000×(1-98%)g×196g/(18×98%) =222.2g =0.222kg 最后可得98%硫酸总质量为x+y=2kg+0.222kg=2.222kg 解法二、设最后可得98%硫酸的质量为x 98%硫酸中:n(H2SO4):n(H2O)=98/98:2/18=1:1/9,则 H2SO4可表示为SO3•H2O 98%H2SO4可表示为SO3•10/9H2O H2SO4•SO3可表示为2SO3•H2O SO3•10/9H2O-吸收过程由水决定-10/9(2SO3•H2O)-稀释过程由SO3决定-20/9(SO3•10/9H2O) SO3•10/9H2O------20/9(SO3•10/9H2O) 100g (20×100/9)g 1000g x X=1000g×(20×100/9)g/100g≈2222g=2.222kg
12、(2010年宁德市)(本题满分13分)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.
⑴ 求证:△AMB≌△ENB;
⑵ ①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并说明理由;
⑶ 当AM+BM+CM的最小值为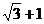 时,求正方形的边长.
时,求正方形的边长.
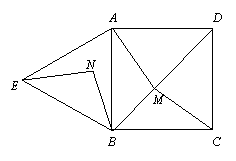
[答案]解:⑴∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°.
∵∠MBN=60°,
∴∠MBN-∠ABN=∠ABE-∠ABN.
即∠BMA=∠NBE.
又∵MB=NB,
∴△AMB≌△ENB(SAS).
⑵①当M点落在BD的中点时,AM+CM的值最小.
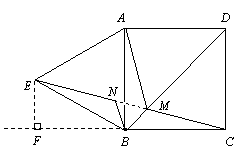 ②如图,连接CE,当M点位于BD与CE的交点处时,
②如图,连接CE,当M点位于BD与CE的交点处时,
AM+BM+CM的值最小. ………………9分
理由如下:连接MN.由⑴知,△AMB≌△ENB,
∴AM=EN.
∵∠MBN=60°,MB=NB,
∴△BMN是等边三角形.
∴BM=MN.
∴AM+BM+CM=EN+MN+CM.
根据“两点之间线段最短”,得EN+MN+CM=EC最短
∴当M点位于BD与CE的交点处时,AM+BM+CM的值最小,即等于EC的长.
⑶过E点作EF⊥BC交CB的延长线于F,
∴∠EBF=90°-60°=30°.
设正方形的边长为x,则BF=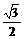 x,EF=
x,EF=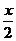 .
.
在Rt△EFC中,
∵EF2+FC2=EC2,
∴(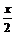 )2+(
)2+(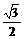 x+x)2=
x+x)2=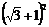 .
.
解得,x=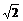 (舍去负值).
(舍去负值).
∴正方形的边长为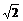 .
.
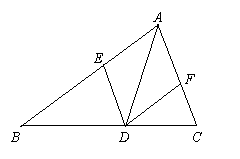
11、(2010年宁德市)(本题满分8分)如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明.
[答案]解法一:添加条件:AE=AF,
 证明:在△AED与△AFD中,
证明:在△AED与△AFD中,
∵AE=AF,∠EAD=∠FAD,AD=AD,
∴△AED≌△AFD(SAS).
解法二:添加条件:∠EDA=∠FDA,
证明:在△AED与△AFD中,
∵∠EAD=∠FAD,AD=AD,∠EDA=∠FDA,
∴△AED≌△AFD(ASA).
10、(2010年浙江省绍兴市) (1) 如图1,在正方形ABCD中,点E,F分别在边BC,
CD上,AE,BF交于点O,∠AOF=90°.
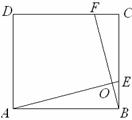 求证:BE=CF.
求证:BE=CF.
|
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,
BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF
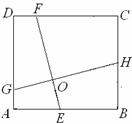 =4.求GH的长.
=4.求GH的长.
|
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,
∠FOH=90°,EF=4. 直接写出下列两题的答案:
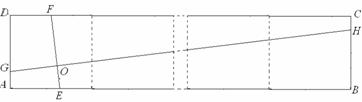
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;
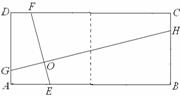
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).
|
|||
|
|||
[答案]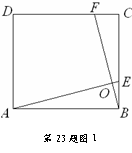 (1) 证明:如图1,∵ 四边形ABCD为正方形,
(1) 证明:如图1,∵ 四边形ABCD为正方形,
∴ AB=BC,∠ABC=∠BCD=90°,
∴ ∠EAB+∠AEB=90°.
∵ ∠EOB=∠AOF=90°,
∴ ∠FBC+∠AEB=90°,∴ ∠EAB=∠FBC,
∴ △ABE≌△BCF , ∴ BE=CF.
(2) 解:如图2,过点A作AM//GH交BC于M,
过点B作BN//EF交CD于N,AM与BN交于点O/,
则四边形AMHG和四边形BNFE均为平行四边形,
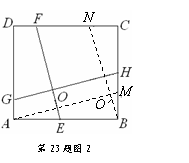 ∴ EF=BN,GH=AM,
∴ EF=BN,GH=AM,
∵ ∠FOH=90°, AM//GH,EF//BN, ∴ ∠NO/A=90°,
故由(1)得, △ABM≌△BCN, ∴ AM=BN,
∴ GH=EF=4.
(3) ① 8.② 4n.
9、(2010重庆市潼南县) 如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2 , ∠3=∠4.
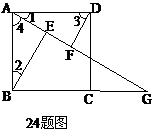 (1)证明:△ABE≌△DAF;
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
解:(1)∵四边形ABCD是正方形
∴AB=AD
在△ABE和△DAF中
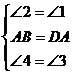
∴△ABE≌△DAF-----------------------4分
(2)∵四边形ABCD是正方形
∴∠1+∠4=900
∵∠3=∠4
∴∠1+∠3=900
∴∠AFD=900----------------------------6分
在正方形ABCD中, AD∥BC
∴∠1=∠AGB=300
在Rt△ADF中,∠AFD=900 AD=2
∴AF=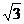 DF
=1----------------------------------------8分
DF
=1----------------------------------------8分
由(1)得△ABE≌△ADF
∴AE=DF=1
∴EF=AF-AE=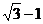 ------------------------10分
------------------------10分
8、(2010重庆潼南县)19.(6分)画一个等腰△ABC,使底边长BC=a,底边上的高为h(要求:用尺规作图,保留作图痕迹,写出已知,求作,不写作法和证明).
已知:
求作: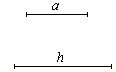
答案:已知:线段a、h
求作:一个等腰△ABC使底边BC=a,底边BC上的高为h
画图(保留作图痕迹图略)
7.(2010日照市)一次函数y=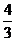 x+4分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个.
x+4分别交x轴、y轴于A、B两点,在x轴上取一点,使△ABC为等腰三角形,则这样的的点C最多有 个.
答案:4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com