
5、在空间四边形ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF∩HG=M,则点M( ).
(A)一定在AC上 (B)一定在BD上
(C)可能在AC上,也可能在BD上 (D)既不在AC上,也不在BD上
4、已知M表示平面,a、b表示直线,给出下面四个命题:
①若a//b,a⊥M,则b⊥M; ②若a⊥M,b⊥M,则a//b;
③若a⊥M,a⊥b,则b//M; ④若a//M ,a⊥b,则b⊥M.
其中正确的命题的选项是( ).
(A) ①② (B) ①②③ (C) ②③④ (D) ①②④
3、已知直线a 平面α,则直线b//a是b//α的( ).
平面α,则直线b//a是b//α的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
2、若a、b、c为三条直线,且a⊥c,b⊥c,则a、b位置关系是( ).
(A) 相交 (B)平行 (C)异面 (D)相交、平行或异面
1、一条直线和梯形两腰垂直,则这条直线和底边的位置关系是( ).
(A)相交不垂直 (B)平行 (C)垂直 (D)不确定
21.解:
(Ⅰ)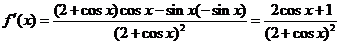 .·································· 2分
.·································· 2分
当 (
(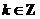 )时,
)时,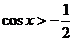 ,即
,即 ;
;
当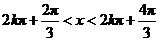 (
(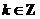 )时,
)时,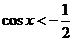 ,即
,即 .
.
因此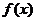 在每一个区间
在每一个区间 (
(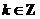 )是增函数,
)是增函数,
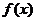 在每一个区间
在每一个区间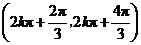 (
(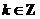 )是减函数.·································· 6分
)是减函数.·································· 6分
(Ⅱ)令 ,则
,则
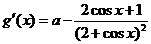
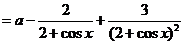
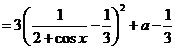 .
.
故当 时,
时,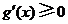 .
.
又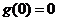 ,所以当
,所以当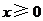 时,
时,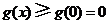 ,即
,即 .···························· 9分
.···························· 9分
当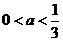 时,令
时,令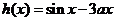 ,则
,则 .
.
故当 时,
时,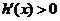 .
.
因此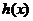 在
在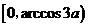 上单调增加.
上单调增加.
故当 时,
时, ,
,
即 .
.
于是,当 时,
时, .
.
当 时,有
时,有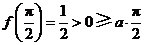 .
.
因此,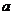 的取值范围是
的取值范围是 . 12分
. 12分
21.(Ⅰ)解:依题设得椭圆的方程为 ,
,
直线 的方程分别为
的方程分别为 ,
, .············································ 2分
.············································ 2分
如图,设 ,其中
,其中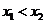 ,
,
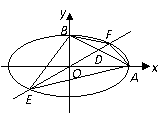 且
且 满足方程
满足方程 ,
,
故 .①
.①
由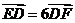 知
知 ,得
,得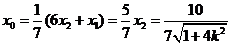 ;
;
由 在
在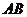 上知
上知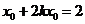 ,得
,得 .
.
所以 ,化简得
,化简得 ,
,
解得 或
或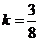 .···································································································· 6分
.···································································································· 6分
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点 到
到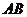 的距离分别为
的距离分别为 ,
,
 .································································ 9分
.································································ 9分
又 ,所以四边形
,所以四边形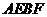 的面积为
的面积为



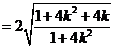
 ,
,
当 ,即当
,即当 时,上式取等号.所以
时,上式取等号.所以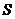 的最大值为
的最大值为 .····························· 12分
.····························· 12分
解法二:由题设, ,
, .
.
设 ,
, ,由①得
,由①得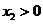 ,
,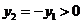 ,
,
故四边形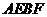 的面积为
的面积为
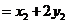 ···················································································································· 9分
···················································································································· 9分



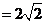 ,
,
当 时,上式取等号.所以
时,上式取等号.所以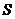 的最大值为
的最大值为 .·············································· 12分
.·············································· 12分
20.解:
(Ⅰ)依题意, ,即
,即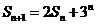 ,
,
由此得 .··················································································· 4分
.··················································································· 4分
因此,所求通项公式为
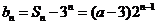 ,
,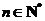 .①········································································ 6分
.①········································································ 6分
(Ⅱ)由①知 ,
,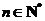 ,
,
于是,当 时,
时,


 ,
,

 ,
,
当 时,
时,
 .又
.又 .
.
综上,所求的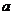 的取值范围是
的取值范围是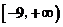 .··································································· 12分
.··································································· 12分
18.解法一:
依题设知 ,
, .
.
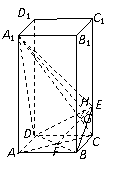
(Ⅰ)连结 交
交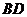 于点
于点 ,则
,则 .
.
由三垂线定理知, .····················································································· 3分
.····················································································· 3分
 在平面
在平面 内,连结
内,连结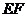 交
交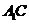 于点
于点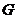 ,
,
由于 ,
,
故 ,
,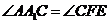 ,
,
 与
与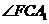 互余.
互余.
于是 .
.
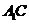 与平面
与平面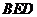 内两条相交直线
内两条相交直线 都垂直,
都垂直,
所以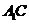
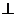 平面
平面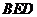 .······························································································· 6分
.······························································································· 6分
(Ⅱ)作 ,垂足为
,垂足为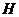 ,连结
,连结 .由三垂线定理知
.由三垂线定理知 ,
,
故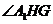 是二面角
是二面角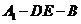 的平面角.································································· 8分
的平面角.································································· 8分
 ,
,
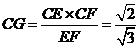 ,
,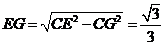 .
.
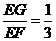 ,
, .
.
又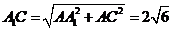 ,
,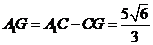 .
.
 .
.
 所以二面角
所以二面角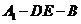 的大小为
的大小为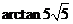 .·························································· 12分
.·························································· 12分
解法二:
以 为坐标原点,射线
为坐标原点,射线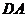 为
为 轴的正半轴,
轴的正半轴,
建立如图所示直角坐标系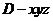 .
.
依题设, .
.
 ,
,
 .················································································ 3分
.················································································ 3分
(Ⅰ)因为 ,
, ,
,
故 ,
, .
.
又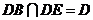 ,
,
所以 平面
平面 .································································································ 6分
.································································································ 6分
(Ⅱ)设向量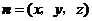 是平面
是平面 的法向量,则
的法向量,则
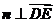 ,
, .
.
故 ,
,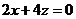 .
.
令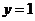 ,则
,则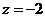 ,
, ,
,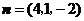 .······························································ 9分
.······························································ 9分
 等于二面角
等于二面角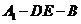 的平面角,
的平面角,
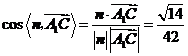 .
.
所以二面角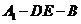 的大小为
的大小为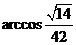 .························································· 12分
.························································· 12分
17.解:
各投保人是否出险互相独立,且出险的概率都是 ,记投保的10 000人中出险的人数为
,记投保的10 000人中出险的人数为 ,
,
则 .
.
(Ⅰ)记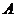 表示事件:保险公司为该险种至少支付10
000元赔偿金,则
表示事件:保险公司为该险种至少支付10
000元赔偿金,则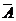 发生当且仅当
发生当且仅当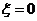 , 2分
, 2分


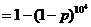 ,又
,又 ,
,
故 .·············································································································· 5分
.·············································································································· 5分
(Ⅱ)该险种总收入为 元,支出是赔偿金总额与成本的和.
元,支出是赔偿金总额与成本的和.
支出
 ,
,
盈利
 ,
,
盈利的期望为  ,················································· 9分
,················································· 9分
由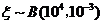 知,
知, ,
,
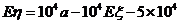
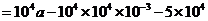 .
.

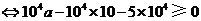
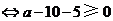
 (元).
(元).
故每位投保人应交纳的最低保费为15元.··································································· 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com