
86、(上海市部分重点中学2008届高三第二次联考)在长方体 中(如图),
中(如图),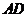 =
=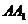 =1,
=1,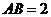 ,点E是AB上的动点
,点E是AB上的动点
(1)若直线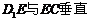 ,请你确定点
,请你确定点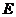 的位置,并求出此时异面直线
的位置,并求出此时异面直线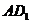 与
与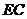 所成的角
所成的角
 (2) 在(1)的条件下求二面角
(2) 在(1)的条件下求二面角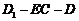 的大小
的大小
[解]解法1:由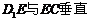
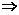 DE与CE垂直-----1分
DE与CE垂直-----1分
设AE=x,在直角三角形DEC中求得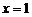 -----2分
-----2分
所以点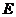 是AB的中点--------------3分
是AB的中点--------------3分
取CD的中点Q,则AQ平行与EC,所以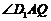 是所求的角------4分
是所求的角------4分
求解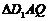 得
得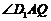 =
=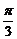 -------------5分
-------------5分
异面直线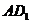 与EC所成的角为
与EC所成的角为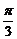 -------6分
-------6分
解法2:利用向量法
分别以DA,DC,D 所在的直线为X轴建立坐标系---------------------------------1分
所在的直线为X轴建立坐标系---------------------------------1分
设AE=x, 根据直线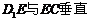
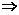
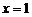 -----2分
-----2分
所以点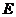 是AB的中点--------------3分
是AB的中点--------------3分
写出A(1,0,0) E(1,1,0 ) C (0,2,0)  (0,0,1)---------4分
(0,0,1)---------4分
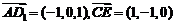
设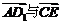 的夹角为
的夹角为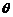 cos
cos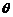 =
= ----------------5分
----------------5分
异面直线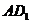 与
与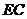 所成的角为
所成的角为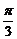 -----------6分
-----------6分
(2)解法1:由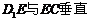
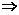 DE与CE垂直,
DE与CE垂直,
所以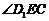 是所求
是所求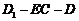 的平面角---8分
的平面角---8分
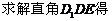
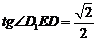 -------11分
-------11分
二面角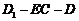 是
是 --------12分
--------12分
解法2:利用向量法求得二面角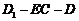 是
是
85、(山西大学附中2008届二月月考)如图,正三棱柱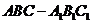 所有棱长都是
所有棱长都是 ,
,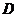 是棱
是棱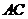 的中点,
的中点,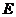 是棱
是棱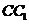 的中点,
的中点,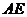 交
交 于点
于点
(1)求证: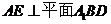 ;
;
(2)求二面角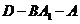 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(3)求点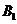 到平面
到平面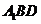 的距离.
的距离.
(1)证明:建立如图所示,
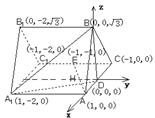
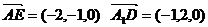

∵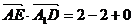
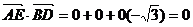
∴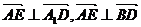 即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
(2)设面DA1B的法向量为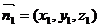
由 ∴取
∴取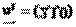
设面AA1B的法向量为 
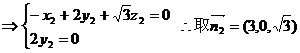 ,
,
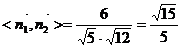
由图可知二面角D-BA1-A为锐角,∴它的大小为arcos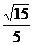
(3) ,平面A1BD的法向量取
,平面A1BD的法向量取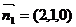
则B1到平面A1BD的距离d=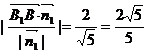
84、
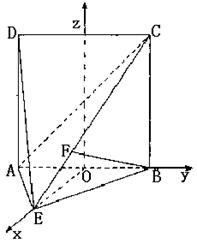
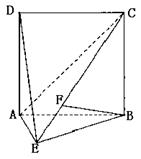 (山东省郓城一中2007-2008学年第一学期期末考试)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F
(山东省郓城一中2007-2008学年第一学期期末考试)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F
为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的余弦值;
(Ⅲ)求点D到平面ACE的距离.
(Ⅳ)求证:平面BDF⊥平面ABCD
解法一:(Ⅰ)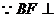 平面ACE.
平面ACE. 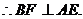
∵二面角D-AB-E为直二面角,且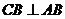 ,
, 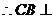 平面ABE.
平面ABE.
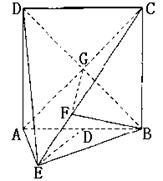

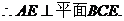
(Ⅱ)连结BD交AC于C,连结FG,
∵正方形ABCD边长为2,∴BG⊥AC,BG=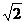 ,
,
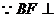 平面ACE,
平面ACE,
(Ⅲ)过点E作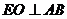 交AB于点O. OE=1.
交AB于点O. OE=1.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,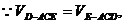
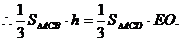
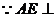 平面BCE,
平面BCE,

 ∴点D到平面ACE的距离为
∴点D到平面ACE的距离为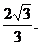
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直
线为x轴,AB所在直线为y轴,过O点平行
于AD的直线为z轴,建立空间直角坐标系
O-xyz,如图.
 面BCE,BE
面BCE,BE 面BCE,
面BCE, 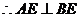 ,
,
在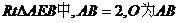 的中点,
的中点,
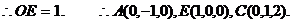
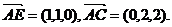 设平面AEC的一个法向量为
设平面AEC的一个法向量为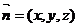 ,
,
则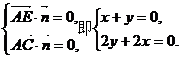 解得
解得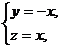
令 得
得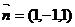 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为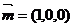 ,
,
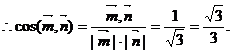 ∴二面角B-AC-E的大小为
∴二面角B-AC-E的大小为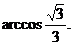
(III)∵AD//z轴,AD=2,∴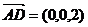 ,
,
∴点D到平面ACE的距离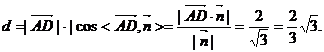
83、(山东省实验中学2008届高三第三次诊断性测试)如图,正方形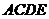 所在的平面与平面
所在的平面与平面 垂直,
垂直,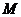 是
是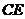 和
和 的交点,
的交点,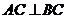 ,且
,且 .
.
(1)求证: 平面
平面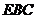 ;
;
(2)求直线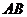 与平面
与平面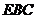 所成的角的大小;
所成的角的大小;
(3)求二面角 的大小.
的大小.
解法一:(Ⅰ)∵四边形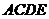 是正方形,
是正方形,
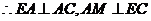 . ………………………1分
. ………………………1分
∵平面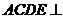 平面
平面 ,又∵
,又∵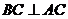 ,
,
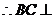 平面
平面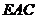 .
……………………2分
.
……………………2分
 平面
平面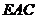 ,
,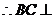
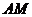 .……………3分
.……………3分
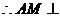 平面
平面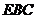 .
………………4分
.
………………4分
(Ⅱ)连结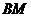 ,
,
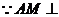 平面
平面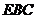 ,
,
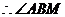 是直线
是直线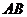 与平面
与平面 所成的角. ………5分
所成的角. ………5分
设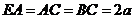 ,则
,则
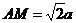 ,
,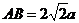 , ………………………6分
, ………………………6分
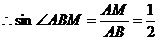 ,
, 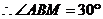 .
.
即直线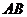 与平面
与平面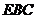 所成的角为
所成的角为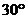 …8分
…8分
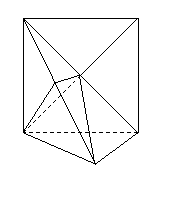 (Ⅲ)过
(Ⅲ)过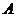 作
作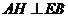 于
于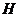 ,连结
,连结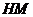 . ……………………9分
. ……………………9分
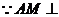 平面
平面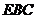 ,
, .
.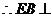 平面
平面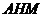 .
.
 是二面角
是二面角 的平面角. ……10分
的平面角. ……10分
∵平面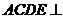 平面
平面 ,
,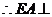 平面
平面 .
.
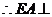
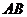 .
.
在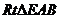 中,
中, 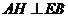 ,有
,有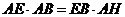 .
.
由(Ⅱ)所设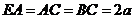 可得
可得
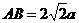 ,
,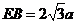 ,
,
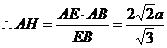 . ………………10分
. ………………10分
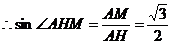 .
.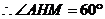 .
.
∴二面角 等于
等于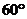 . ……………………12分
. ……………………12分
解法二: ∵四边形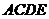 是正方形 ,
是正方形 ,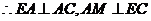 ,
,
∵平面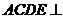 平面
平面 ,
,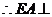 平面
平面 , ………2分
, ………2分
 ∴可以以点
∴可以以点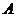 为原点,以过
为原点,以过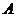 点平行于
点平行于 的直线为
的直线为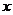 轴,
轴,
分别以直线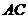 和
和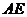 为
为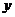 轴和
轴和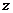 轴,建立如图所示的空
轴,建立如图所示的空
间直角坐标系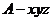 .
.
设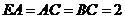 ,则
,则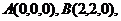
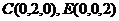 ,
,
 是正方形
是正方形 的对角线的交点,
的对角线的交点,
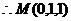 .……………4分
.……………4分
(Ⅰ)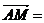
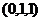 ,
,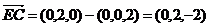 ,
,
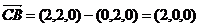 ,
,
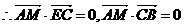 , ……………………………………4分
, ……………………………………4分
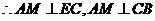
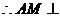 平面
平面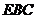 . ………………5分
. ………………5分
(Ⅱ)
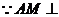 平面
平面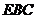 ,
, 为平面
为平面 的一个法向量,…………6分
的一个法向量,…………6分
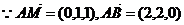 ,
,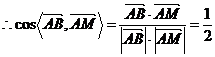 .……………7分
.……………7分
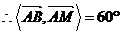 .∴直线
.∴直线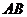 与平面
与平面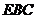 所成的角为
所成的角为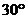 . ……8分
. ……8分
(Ⅲ) 设平面 的法向量为
的法向量为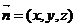 ,则
,则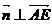 且
且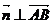 ,
,
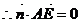 且
且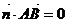 .
.
 即
即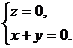
取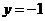 ,则
,则 , 则
, 则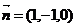 .………………10分
.………………10分
又∵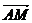 为平面
为平面 的一个法向量,且
的一个法向量,且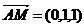 ,
,
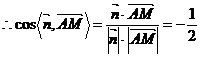 ,设二面角
,设二面角 的平面角为
的平面角为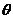 ,则
,则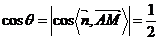 ,
,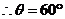 .∴二面角
.∴二面角 等于
等于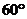 .…12分
.…12分
82、(山东省聊城市2008届第一期末统考)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=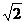 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
(1)求证:AM//平面BDE;
(2)求二面角A-DF-B的大小.
(1)解:记AC与BD的交点为O,连接OE………………1分
∵O,M分别是AC、EF的中点,且四边形ACEF是矩形,
∴四边形AOEM是平行四边形,
∴AM//OE,
 又OE
又OE 平面BDE,AM
平面BDE,AM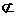 平面BDE,
平面BDE,
∴AM//平面BDE.……………………4分
(2)在平面AFD中过A作AS⊥DF,垂足为S,连接BS,
∵AB⊥AF,AB⊥AD,AD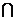 AF=A,
AF=A,
∴AB⊥平面ADF.…………………………6分
又DF 平面ADF,
平面ADF,
∴DF⊥AB,又DF⊥AS,AB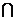 AS=A,
AS=A,
∴DF⊥平面ABS.
又BS 平面ABS,
平面ABS,
∴DF⊥SB.
∴∠BSA是二面角A-DF-B的平面角.……………………8分
在Rt△ASB中,AS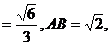
∴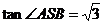
∴∠ASB=60°.……………………………………10分
(本题若利用向量求解可参考给分)
81、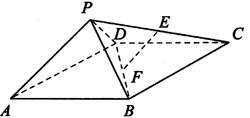 (山东省济南市2008年2月高三统考)如图,四棱锥P-ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(山东省济南市2008年2月高三统考)如图,四棱锥P-ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求锐二面角B-PD-C的余弦值.
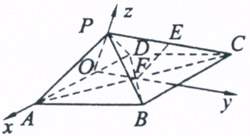 解:(1)如图,连接AC,
解:(1)如图,连接AC,
∵ABCD为矩形且F是BD的中点,
∴AC必经过F 1分
又E是PC的中点,
所以,EF∥AP 2分
∵EF在面PAD外,PA在面内,
∴EF∥面PAD 4分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD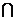 面ABCD=AD,∴CD⊥面PAD,
面ABCD=AD,∴CD⊥面PAD,
又AP 面PAD,∴AP⊥CD 6分
面PAD,∴AP⊥CD 6分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD 7分
又AD 面PAD,所以,面PDC⊥面PAD 8分
面PAD,所以,面PDC⊥面PAD 8分
(3)由P作PO⊥AD于O,以OA为x轴,以OF为y轴,以OP为z轴,则
A(1,0,0),P(0,0,1) 9分
由(2)知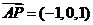 是面PCD的法向量,B(1,1,0),D(一1,0,0),
是面PCD的法向量,B(1,1,0),D(一1,0,0),
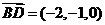 ,
,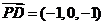 10分
10分
设面BPD的法向量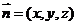 ,
,
由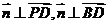 得
得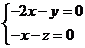
取 ,则
,则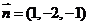 ,
,
向量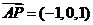 和
和 的夹角的余弦
的夹角的余弦 11分
11分
所以,锐二面角B-PD-C的余弦值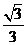 12分
12分
80、(宁夏区银川一中2008届第六次月考)如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,截面DAN交PC于M.
(Ⅰ)求PB与平面ABCD所成角的大小;
(Ⅱ)求证:PB⊥平面ADMN;
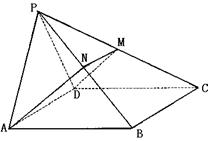 (Ⅲ)求以AD为棱,PAD与ADMN为面的二面角的大小.
(Ⅲ)求以AD为棱,PAD与ADMN为面的二面角的大小.
(I)解:取AD中点O,连结PO,BO.
△PAD是正三角形,所以PO⊥AD,…………1分
又因为平面PAD⊥平面ABCD,
所以,PO⊥平面ABCD, …………3分
BO为PB在平面ABCD上的射影,
所以∠PBO为PB与平面ABCD所成的角.…………4分
由已知△ABD为等边三角形,所以PO=BO=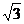 ,
,
所以PB与平面ABCD所成的角为45°. ………………5分
(Ⅱ)△ABD是正三角形,所以AD⊥BO,所以AD⊥PB, ………………6分
又,PA=AB=2,N为PB中点,所以AN⊥PB, ………………8分
所以PB⊥平面ADMN. ………………9分
(Ⅲ)连结ON,因为PB⊥平面ADMN,所以ON为PO在平面ADMN上的射影,
因为AD⊥PO,所以AD⊥NO, ………………11分
故∠PON为所求二面角的平面角.
因为△POB为等腰直角三角形,N为斜边中点,所以∠PON=45°……………12分
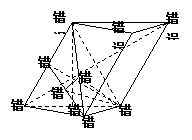
79、(江西省鹰潭市2008届高三第一次模拟)已知斜三棱柱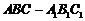 ,
,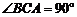 ,
, ,
,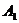 在底面
在底面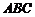 上的射影恰为
上的射影恰为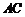 的中点
的中点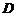 ,又知
,又知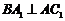 .
.
(Ⅰ)求证: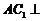 平面
平面 ;
;
(Ⅱ)求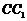 到平面
到平面 的距离;
的距离;
(Ⅲ)求二面角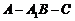 的大小.
的大小.
解法 :(Ⅰ)∵
:(Ⅰ)∵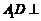 平面
平面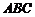 ,∴平面
,∴平面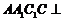 平面
平面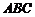 ,
,
又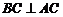 ,∴
,∴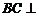 平面
平面 , 得
, 得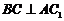 ,又
,又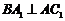 ,
,
 ∴
∴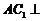 平面
平面 .…………………4分
.…………………4分
(Ⅱ)∵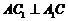 ,四边形
,四边形 为菱形,故
为菱形,故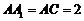 ,
,
又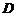 为
为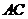 中点,知∴
中点,知∴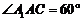 .取
.取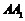 中点
中点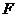 ,则
,则
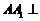 平面
平面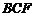 ,从而面
,从而面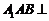 面
面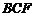 ,…………6分
,…………6分
过 作
作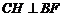 于
于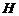 ,则
,则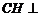 面
面 ,在
,在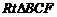 中,
中,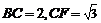 ,故
,故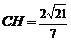 ,即
,即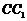 到平面
到平面 的距离为
的距离为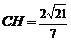 .…………………8分
.…………………8分
(Ⅲ)过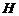 作
作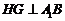 于
于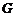 ,连
,连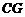 ,则
,则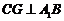 ,从而
,从而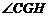 为二面角
为二面角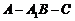 的平面角,在
的平面角,在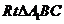 中,
中,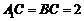 ,∴
,∴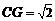 ,…………10分
,…………10分
在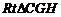 中,
中,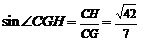 ,故二面角
,故二面角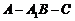 的大小为
的大小为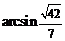 .
.
…………………12分
 解法
解法 :(Ⅰ)如图,取
:(Ⅰ)如图,取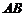 的中点
的中点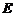 ,则
,则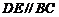 ,∵
,∵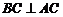 ,∴
,∴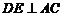 ,
,
又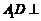 平面
平面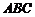 ,以
,以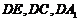 为
为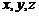 轴建立空间坐标系, …………1分
轴建立空间坐标系, …………1分
则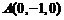 ,
,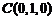 ,
,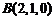 ,
,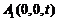 ,
,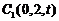 ,
,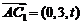 ,
,
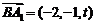 ,
,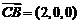 ,由
,由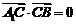 ,知
,知 ,
,
又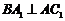 ,从而
,从而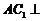 平面
平面 .…………………4分
.…………………4分
(Ⅱ)由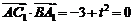 ,得
,得 .设平面
.设平面 的法向量
的法向量
为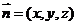 ,
,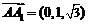 ,
,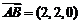 ,
,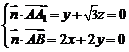 ,
,
设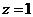 ,则
,则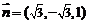 .…………6分
.…………6分
∴点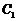 到平面
到平面 的距离
的距离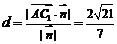 .…………………8分
.…………………8分
(Ⅲ)设面 的法向量为
的法向量为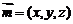 ,
,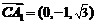 ,
,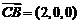 ,
,
∴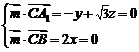 .…………10分
.…………10分
设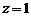 ,则
,则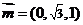 ,故
,故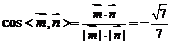 ,根据法向量的方向
,根据法向量的方向
可知二面角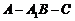 的大小为
的大小为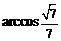 .…………………12分
.…………………12分
78、(江苏省南通通州市2008届高三年级第二次统一测试)如图已知在三棱柱ABC--A1B1C1中,AA1⊥面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
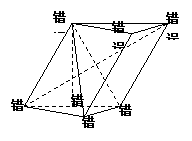 (1)求证:面PCC1⊥面MNQ;
(1)求证:面PCC1⊥面MNQ;
(2)求证:PC1∥面MNQ.
主要得分步骤:(1)AB⊥面PCC1; 4′
MN∥AB,故MN⊥面MNQ
MN在平面MNQ内,∴面PCC1⊥面MNQ; 7′
(2)连AC1、BC1,BC1∥NQ,AB∥MN
面ABC1∥面MNQ 11′
PC1在面ABC1内.
∴PC1∥面MNQ. 13′
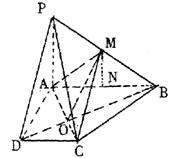
77、(江苏省泰兴市2007-2008学年第一学期高三调研)已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC=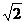 ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
(Ⅰ)证明:平面PAD⊥PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分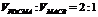 ;
;
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线PD
是否平行面AMC.
(I)证明:依题意知: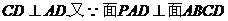
 …………2分
…………2分
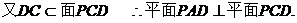 …4分
…4分
(II)由(I)知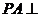 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD. …………5分
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则
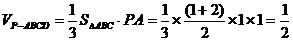 …………8分
…………8分
要使
即M为PB的中点. …………10分
(Ⅲ)连接BD交AC于O,因为AB//CD,AB=2,CD=1,由相似三角形易得BO=2OD
∴O不是BD的中心……………………10分
又∵M为PB的中点
∴在△PBD中,OM与PD不平行
∴OM所以直线与PD所在直线相交
又OM 平面AMC
平面AMC
∴直线PD与平面AMC不平行.……………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com