1．某地区有300家商店，其中大型商店30家，中型商店75家，小型商店175家，为了掌握各商店的营业情况，要从中抽取一个容量为20的样本．若采用分层抽样的方法，抽到的中型商店数是

(　)

A．2　　　　　　　　　　　　　 B．3

C．5　 　　　　　　　　　　　　　　　　　　　　　　 D．13

解析：根据分层抽样按比例抽取，抽取的比例为＝，抽取的中型商店数为75×＝5.

答案：C

21．已知圆C：x²+y²－2x+4y－4＝0是否存在斜率为1的直线l，使以l被圆C截得弦AB为直径的圆经过原点？若存在，写出直线l的方程，若不存在说明理由．

20．已知点T是半圆O的直径AB上一点，AB＝2，OT＝t(0<t<1)以AB为腰作直角梯形AA'B'B，使AA'垂直且等于AT，使BB'垂直且等于BT，A'B'交半圆于P、Q两点，如图所示的直角坐标系．

　　 ⑴ 写出直线A'B'的方程．

⑵ 计算出点P、Q的坐标．

⑶ 证明：由点P发出的光线入射点为T，经AB反射后，反射光线通过点Q．

19．要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格小钢板的块数如下表，每张钢板的面积为：第一种1m²，第二种2m²，今需要A、B、C三种规格的成品分别为12、15、17块，问分别截这两种钢板多少张可得符合上面要求的三种规格产品，且使所用钢板总面积最小？

18．已知圆x²+y²＝9的内接△ABC中， A点的坐标是(－3，0)，重心G的坐标是(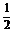－，－1)求：

(1) 直线BC的方程；

(2) 弦BC的长度．

17．直线l过点(1，1)交x轴、y轴的正半轴分别于点A、B，由A、B作直线2x+y+3＝0的垂线，垂足分别为C、D，当|CD|最小时，求l的方程．

16．直线l被两条平行直线l₁：x+2y－1＝0及l₂：x+2y－3＝0所截线段的中点在直线x－y－1＝0上，且l到直线x+2y－3＝0的角为45°，求直线l的方程．

15．在圆x²+y²－5x＝0内，过点(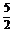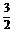，) 有n条长度成等差数列的弦， 最小弦为a₁最大弦为a_n若公差d∈[，]，那么n的取值集合是　　　　 　．

14．圆心在y轴上，且与直线x+y－3＝0及x－y－1＝0都相切的圆的方程为　　　　　　 ．

13．将一张画有直角坐标系的图纸折叠一次，使得点A(0，2)与点B(4，0)重合，若此时点C(7，3)与点D(m，n)重合，则m+n的值是　　　　 ．