
21.解:(1)要使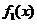 与
与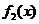 有意义,则有
有意义,则有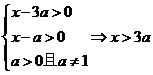

要使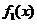 与
与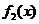 在给定区间[a + 2,a + 3]上有意义,等价于真数的最小值大于0
在给定区间[a + 2,a + 3]上有意义,等价于真数的最小值大于0
即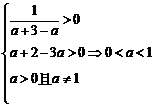
(2) 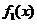 与
与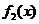 在给定区间[a + 2,a + 3]上是接近的
在给定区间[a + 2,a + 3]上是接近的
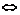
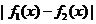 ≤1
≤1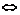
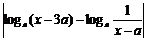 ≤1
≤1 |loga[(x – 3a)(x – a)]|≤1
|loga[(x – 3a)(x – a)]|≤1
 a≤(x – 2a)2 – a2≤
a≤(x – 2a)2 – a2≤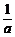
对于任意x∈[a + 2,a + 3]恒成立
设h(x) = (x – 2a)2 – a2,x∈[a + 2,a + 3]
且其对称轴x = 2a < 2在区间[a + 2,a + 3]的左边
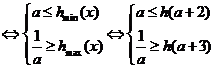
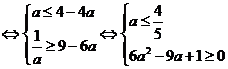
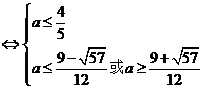
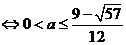
当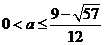 时,
时,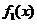 与
与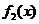 在给定区间[a + 2,a + 3]上是接近的
在给定区间[a + 2,a + 3]上是接近的
当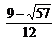 < a < 1时,
< a < 1时,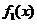 与
与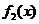 在给定区间[a + 2,a + 3]上是非接近的.
在给定区间[a + 2,a + 3]上是非接近的.
19.解:(1)函数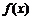 在[– 1,1]上是增函数
在[– 1,1]上是增函数
设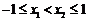
∵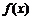 是定义在[–1,1]上的奇函数,∴ f(x2)-f(x1 )= f(x2 )+ f(–
x1).
是定义在[–1,1]上的奇函数,∴ f(x2)-f(x1 )= f(x2 )+ f(–
x1).
又x1 < x2,∴ x2 +(– x1)≠0,
由题设有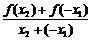 >0,
>0,
∵ x2 + (– x1) = x2-x1>0,∴ f ( x2 ) + f (– x1)>0,即f ( x1 )< f ( x2 ),
所以函数f (x) 在[– 1,1]上是增函数. 4分
(2)不等式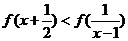
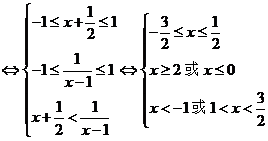
解得: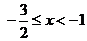
(3)由(1)知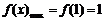 ,∴
,∴ 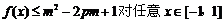 恒成立
恒成立
只需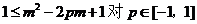 恒成立,即
恒成立,即 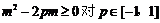 恒成立
恒成立
设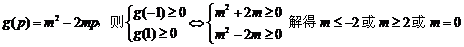
∴ m的取值范围是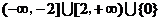
20解:(1)当a=0时,函数f(-x)=(-x)2+|-x|+1=f(x),此时f(x)为偶函数.
当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a),f(-a)≠-f(a).
此时函数f(x)既不是奇函数,也不是偶函数
(2)①当x≤a时,函数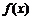 =x2-x+a+1=(x-
=x2-x+a+1=(x-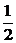 )2+a+
)2+a+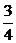 .
.
若a≤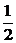 ,则函数
,则函数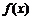 在(-∞,a]上单调递减,从而,函数
在(-∞,a]上单调递减,从而,函数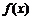 在(-∞,a]上的最小值为f(a)=a2+1.
在(-∞,a]上的最小值为f(a)=a2+1.
若a>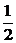 ,则函数f(x)在(-∞,a
,则函数f(x)在(-∞,a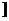 上的最小值为f(
上的最小值为f(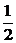 )=
)=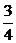 +a,且f(
+a,且f(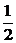 )≤f(a).
)≤f(a).
②当x≥a时,函数f(x)=x2+x-a+1=(x+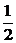 )2-a+
)2-a+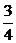 .
.
若a≤-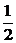 ,则函数f(x)在[a,+∞
,则函数f(x)在[a,+∞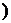 上的最小值为f(-
上的最小值为f(-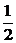 )=
)=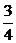 -a,且f(-
-a,且f(-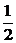 )≤f(a).
)≤f(a).
若a>-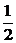 ,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞)上的最小值为f(a)=a2+1.
,则函数f(x)在[a,+∞)上单调递增,从而,函数f(x)在[a,+∞)上的最小值为f(a)=a2+1.
综上,当a≤-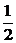 时,函数f(x)的最小值是
时,函数f(x)的最小值是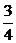 -a.
-a.
当-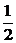 <a≤
<a≤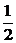 时,函数f(x)的最小值是a2+1.
时,函数f(x)的最小值是a2+1.
当a>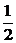 时,函数f(x)的最小值是a+
时,函数f(x)的最小值是a+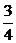 .
.
18.解: 
17.解:(1)原不等式等价于 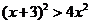
即 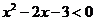 4分
4分
解得 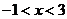 5分
5分
∴ 原不等式的解集为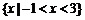 6分
6分
(2)原不等式等价于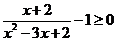
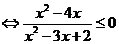
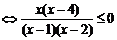 4分
4分
解得 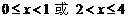 ,
,
∴原不等式的解集为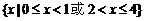 6分
6分
16.解: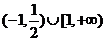
11. 充分不必要 12. 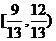 13.
13. 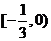 14.
14. 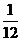 15. ③④
15. ③④
1-10. CDACC CCACC
21.(本小题满分14分)
对于在区间[m,n]上有意义的两个函数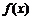 与
与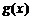 ,如果对任意
,如果对任意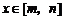 均有
均有 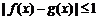 ,则称
,则称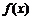 与
与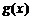 在[m,n]上是接近的,否则称
在[m,n]上是接近的,否则称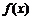 与
与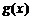 在[m,n]上是非接近的,现有两个函数
在[m,n]上是非接近的,现有两个函数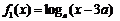 与
与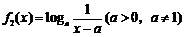 ,给定区间
,给定区间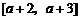 .
.
(1)若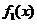 与
与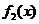 在给定区间
在给定区间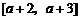 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;
(2)讨论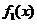 与
与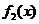 在给定区间
在给定区间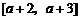 上是否是接近的?
上是否是接近的?
麻城博达学校2010届高三阶段测试(七)
理科数学试题(B卷)
20.(本小题满分13分)
设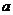 为实数,函数
为实数,函数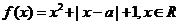 。
。
(1)讨论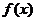 的奇偶性;
的奇偶性;
(2)求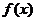 的最小值。
的最小值。
19.(本小题满分12分)
已知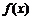 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且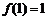 ,若
,若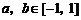 ,
,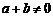 时,有
时,有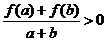 .
.
(1)判断函数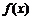 在[-1,1]上是增函数,还是减函数,并证明你的结论;
在[-1,1]上是增函数,还是减函数,并证明你的结论;
(2)解不等式: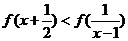 ;
;
(3)若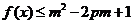 对所有
对所有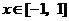 ,
,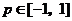 (p是常数)恒成立,求实数m的取值范围.
(p是常数)恒成立,求实数m的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com