2.其实文章的目的绝不仅仅是抒一点儿“真情”就罢，结尾借父亲的口道：“做人也……不能……像盆景中的兰草一样降了品格；低俗的人不会给社会有贡献的。”

--话因“境”造，理自“情”生，语重心长，意味隽永。

[实用兵法]

真情写作　 写出真情

1.由淡淡地讲述访兰到“我再也不敢去挖这些野兰了”，情感发生了突变，是因为父亲的话使“我”猛然识了野兰的“不俗处”。

--“情”因事发，“感”因“物”生，发自“我”心，感于“我”胸，真切、感人。

2.以生活画面的再现唤起记忆，找回忽略的细节感，营造感性氛围，聚合情感，复苏写作的灵感。

[链接]

“感情真挚”考点解说

“感情真挚”是作者在情感表达、展示的过程中做到：具体而不空泛，真实而不虚假，自然而不做作。

要求--

◇在作文中能够自然地表达真情实感，使感情的流露能够给人以真实感、真诚感，而不是附加感、装饰感。

◇喜怒哀乐，真情表露，写实事，讲实话，抒实情，明实理，不人云亦云、随波逐流。

◇展开联想、想象要合情合理，抒发感情要恰如其分。不要为了迎合阅卷老师而矫揉造作，夸大感情，更不能胡编滥造。

[作家在线]

[作家范文]

访 　兰

父亲喜欢兰草，过些日子，就要到深山中一趟，带回些野兰来培栽。几年间，家里庭院就有了百十余品种，像要作一个兰草园圃似的。方圆十几里的人就都跑来观赏，父亲并不因此而得意，反而倒有几分愠怒。以后又进山去，可不再带回那些野生野长的兰草了。这事使我很奇怪，问他，又不肯说，只是有一次再进山的时候，要我和他一块：“访兰去吧！”

我们走了半天，一直到了山的深处。那里有一道瀑布，从几十丈高的山崖直直垂下，老远就听到了轰轰隆隆的响声，水沫扬起来，弥漫了半天，日光在上面浮着，晕出七彩迷丽的虚幻。我们沿谷底走，便看见有很多野兰草，盈尺高的，都开了淡淡的兰花，像就地铺着了一层寒烟；香气浓烈极了，气浪一冲，站在峡谷的任何地方都闻到了。

我从未见过这么清妙的兰草，连声叫好，又动手要挖起一株来，想，父亲会培育这仙品的：以前就这么挖回去，经过一番培栽，就养出了各种各样的品类、形状的呢！

父亲却把我制住了。问道：“你觉得这里的兰草好呢，还是家里的那些好呢？”

我说：“这里的好！”

“怎么好呢？”

我却说不出来。家里的的确比这里的看着好看，这里的却比家里的清爽。“是味儿好像不同吗？”

“是的。”

“这是为什么？一样的兰草，长在两个地方就有两个味儿？”

父亲说：“兰草是空谷的幽物，得的是天地自然的原气，长的是山野水畔的趣姿；一经培栽，便成了玩赏的盆景。”

“但它确实叶更嫩、花更繁更大了呢！”

“样子是似乎美了，但美得太甜、太媚，格调也就俗了。”

父亲的话是对的，但我却不禁惋惜了：这么精神的野兰在这么个空谷僻野，叶是为谁长的，花是为谁开的，会有几个欣赏它呢？

“这正是它的不俗处。它不为被人欣赏而生长，却为着自己的特色而存在着，所以它才长得叶纯，开得花纯，楚楚的有着它的灵性。”

我再也不敢去挖这些野兰了。欣赏它的这种纯朴，后悔以前为什么喜爱着它而却无形中就毁了它呢！

父亲拉我坐在潭边，我们的身影就静静地沉在水里；他看着兰，也在看着我，说：“做人也是这样啊，孩子！人活在世上，不能失了自己的真性，献媚处事，就像盆景中的兰草一样降了品格；低俗的人不会给社会有贡献的。”

我深深地记着父亲的话。从那以后，已经是15年过去了，我一直未敢忘却过。　　　　　　　　　　　　　　　　　　　　 　　　　　　　(贾平凹)

[范文启示]

1.写不好作文不是技巧不够，积累不足，而是“我”不在场。

5. Rt△ABC所在平面外一点S,且SA=SB=SC,点D为斜边AC的中点.

求证:SD⊥平面ABC;

若AB=BC,求证:BD⊥平面SAC

4.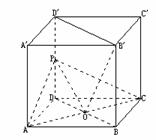如图,在正方体

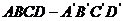
中,P为D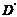 中点,O

为面ABCD的中心,

求证: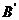O⊥平面PAC

3.如图: △ABC中,

∠B=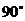,P是△ABC

外一点,且PA=PB,

PB⊥BC,若M是PC

的中点,试确定AB上

点N的位置,使得MN⊥AB

2.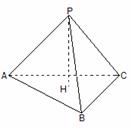如图:已知P是△ABC

所在平面外一点,PA,

PB,PC两两互相垂直,

H是△ABC的垂心,

求证:PH⊥平面ABC

[变式]

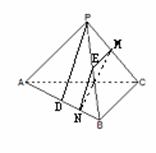
如图:已知P是△ABC所在平面外一点,PA,

PB,PC两两互相垂直,H为垂足

(1)求证:H是△ABC的垂心;

(2)求证: △ABC也是锐角三角形

(3)当PA=PB=b,PA=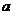时,求P到平面ABC的距离.

[解题思路]

①.利用线面垂直的定义:一直线垂直于平面内的任意一直线,这直线垂直于该平面.

②.用线面垂直的判定定理:一直线垂直于平面内的两相交直线,这直线与平面垂直.

③.证明线线(或线面)垂直,有时需多次运用线面垂直的定义和线面垂直的判定定理,实现线线垂直与线面垂直的相互转化.

④.利用空间向量知识证明:证明直线所对应的向量与平面的法向量平行.

1.设ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC

7.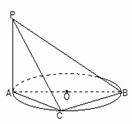如图AB是圆O的

直径,C是异于A,B

的圆周上的任意一

点,PA垂直于圆O

所在的平面,则BC

与PC　　　　　 .

[变式]

在原题的基础上,加上条件:

过A点作AE⊥PC于E,AF⊥PB于F.

(1)求证:AE⊥平面PBC;

(2)求证:EF⊥PB;

(3)这个图形中有多少个线面垂直关系?

(4个线面垂直关系:PA⊥平面ABC,PB⊥平面AEF, AE⊥平面PBC BC⊥平面PAC)