
1.设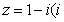 是虚数单位),则
是虚数单位),则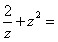
A. B.
B.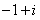 C.
C.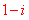 D.
D.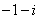
22.(14分)已知椭圆C的中心在原点,焦点在x轴上,一条经过点(3,-)且方向向量为a=(-2,)的直线L交椭圆C于A、B两点交x轴于M点,又=2.
(1)求直线L的方程;
(2)求椭圆C长轴长取值的范围.
解:(1)直线L过点(3,-)且方向向量a=(-2,)
∴L的方程为:=即y=-(x-1)
(2)设直线y=-(x-1)和椭圆+=1
交于两点A(x1,y1),B(x2,y2)和x轴交点M(1,0),由=2,知y1=-2y2.
将x=-y+1代入b2x2+a2y2=a2b2中得
(b2+a2)y2-b2y+b2(1-a2)=0
由韦达定理
∵有两交点,∴Δ=(-b2)2-4(b2+a2)·b2(1-a2)>0,化简得:5a2+4b2>5 ③
由①②消去y2得:32b2=(4b2+5a2)(a2-1)
即4b2=>0 ④
将④代入③得:5a2+>5 ⑤
可求得1<a2<9又椭圆的焦点在x轴上,则a2>b2
∴4b2=<4a2,综合解得:1<a2<
可求得:1<a<
∴所求椭圆长轴长2a的范围是(2,).
21.(12分)神舟6号飞船返回仓顺利到达地球后,为了及时将航天员安全救出,地面指挥中心在返回仓预计到达区域安排三个救援中心(记为A,B,C),A在B的正东方向,相距6千米,C在B的北偏西30°,相距4千米,P为航天员着陆点,某一时刻,A接收到P的求救信号,由于B,C两地比A距P远,因此4秒后,B,C两个救援中心才同时接收到这一信号.已知该信号的传播速度为1千米/秒.
(1)求在A处发现P的方位角;
(2)若信号从P点的正上空Q点处发出,则A,B收到信号时间差变大还是变小,说明理由.
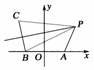
图5
解:(1)如图5,∵|PC|=|PB|,∴P在线段BC的垂直平分线上,又∵|PB|-|PA|
=4,∴P在以A,B为焦点的双曲线的右支上,以AB中点为坐标原点,AB所在直线为x轴建立直角坐标系,则A(3,0),B(-3,0),C(-5,2),
∴双曲线方程为-=1,x>0,
BC的垂直平分线方程为x-y+7=0,
联立两方程解得x=8,
∴P(8,5),kPA=tan∠PAx=,∠PAx=60°,
∴P点在A点的北偏东30°处.
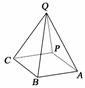
图6
(2)如图6所示,
设|PQ|=h,|PB|=x,|PA|=y,
∵-=-=(x-y)<x-y=-.
故A,B收到信号时间差变小.
20.(12分)设抛物线过定点A(2,0),且以直线x=-2为准线.
(1)求抛物线顶点的轨迹C的方程;
(2)已知点B(0,-5),轨迹C上是否存在满足·=0的M、N两点?证明你的结论.
解:(1)设抛物线顶点为P(x,y),则抛物线的焦点F(2x+2,y),由抛物线定义,可得=4.
∴+=1.
∴轨迹C的方程为+=1(x≠-2).
(2)不存在.
设过点B(0,-5),斜率为k的直线方程为y=kx-5(斜率不存在时,显然不符合题意),
由∴(4+k2)x2-10kx+9=0.
由Δ≥0,得k2≥.
假设在轨迹C上存在两点M、N,令MB、NB的斜率分别为k1、k2,则|k1|≥,|k2|≥.
显然不可能满足k1·k2=-1,
∴轨迹C上不存在满足·=0的两点.
19.(12分)(2010·浙江温州八校联考)已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(,0).
(1)求双曲线C的方程;
(2)若直线l:y=kx+与双曲线C恒有两个不同的交点A和B,且·>2(其中O为原点),求k的取值范围.
解:(1)设双曲线方程为-=1(a>0,b>0).
由已知得a=,c=2,再由a2+b2=22,得b2=1.
故双曲线C的方程为-y2=1.
(2)将y=kx+代入-y2=1,
得(1-3k2)x2-6kx-9=0.
由直线l与双曲线交于不同的两点得
即k2≠且k2<1.①
设A(xA,yA),B(xB,yB),则
xA+xB=,xAxB=.
由·>2得xAxB+yAyB>2,
而xAxB+yAyB=xAxB+(kxA+)(kxB+)
=(k2+1)xAxB+k(xA+xB)+2=(k2+1)+k+2=.
于是>2,即>0,解此不等式得<k2<3.②
由①②得<k2<1.
故k的取值范围为(-1,-)∪(,1).
18.(12分)已知曲线C的方程为kx2+(4-k)y2=k+1(k∈R).
(1)若曲线C是椭圆,求k的取值范围;
(2)若曲线C是双曲线,且有一条渐近线的倾斜角是60°,求此双曲线的方程;
(3)满足(2)的双曲线上是否存在两点P、Q关于直线l:y=x-1对称,若存在,求出过P、Q的直线方程;若不存在,说明理由.
解:(1)当k=0或k=-1或k=4时,C表示直线;
当k≠0且k≠-1且k≠4时方程为
+=1,①
方程①表示椭圆的充要条件是
即是0<k<2或2<k<4.
(2)方程①表示双曲线的充要条件是·<0,
即k<-1或-1<k<0或k>4.
①当k<-1或k>4时,双曲线焦点在x轴上,
a2=,b2=,
其一条渐近线的斜率为==得k=6.
②当-1<k<0时,双曲线焦点在y轴上,
a2=,b2=-,
其一条渐近线的斜率为==,得k=6(舍),
综上得双曲线方程为-=1.
(3)若存在,设直线PQ的方程为:y=-x+m.
由消去y,
得4x2+4mx-2m2-7=0.②
设P、Q的中点是M(x0,y0),则
M在直线l上,
∴=--1,解得m=-,方程②的Δ>0,
∴存在满足条件的P、Q,直线PQ的方程为y=-x-.
17.(12分)求两条渐近线为x+2y=0和x-2y=0且截直线x-y-3=0所得的弦长为的双曲线方程.
解:设所求双曲线的方程为x2-4y2=k(k≠0),
将y=x-3代入双曲线方程得3x2-24x+k+36=0,
由韦达定理得x1+x2=8,x1x2=+12,
由弦长公式得
|x1-x2|=· =,
解得k=4,
故所求双曲线的方程为-y2=1.
16.以下四个关于圆锥曲线的命题:
①设A、B为两个定点,k为非零常数,若||-||=k,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动弦AB,O坐标原点,若=(+),则动点P的轨迹为椭圆;
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
④双曲线-=1与椭圆+y2=1有相同的焦点.
其中真命题的序号为__________.(写出所有真命题的序号)
解析:①当k为负值时,动点轨迹不为双曲线;②当=时,点P不在椭圆上;③④正确,则真命题为③④.
答案:③④
15.过双曲线x2-y2=4的右焦点F作倾斜角为105°的直线交双曲线于P、Q两点,则|FP|·|FQ|的值为__________.
解析:设P(x1,y1),Q(x2,y2),
∵|FP|=ex1-a,|FQ|=ex2-a,
|FP|·|FQ|=(ex1-a)(ex2-a)
=e2x1x2-ae(x1+x2)+a2.
kPQ=tan105°=-(2+).
直线PQ的方程为y=-(2+)(x-2).
由得
x1+x2=,
x1x2=.
∴|FP|·|FQ|=e2x1x2-ae(x1+x2)+a2
=2×-2×+4
=.
答案:
14.过双曲线-=1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于__________.
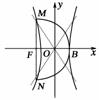
图4
解析:如图4所示,由题意
M(-c,),MF=FB,
即=c+a.①
∵b2=c2-a2,
由①整理得c2-ac-2a2=0,即
(c+a)(c-2a)=0.
∴c=-a(舍)或c=2a.
∴e==2.
答案:2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com