8．(2009·江苏卷)设α和β为不重合的两个平面，给出下列命题：

(1)若α内的两条相交直线分别平行于β内的两条直线，则α平行于β；

(2)若α外一条直线l与α内的一条直线平行，则l和α平行；

(3)设α和β相交于直线l，若α内有一条直线垂直于l，则α和β垂直；

(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直．

上面命题中，真命题的序号________(写出所有真命题的序号)．

[解析]　考查立体几何中的直线、平面的垂直与平行判定的相关定理．真命题的序号是(1)(2)．

[答案]　(1)(2)

7．(2009·安徽卷文)在平行四边形ABCD中，E和F分别是边CD和BC的中点，或＝λ+μ，其中λ、μ∈R，则λ+μ＝________.

[解析]　设＝b、＝a，则＝b－a，＝b－a，＝b－a，代入条件得λ＝μ＝，∴λ+μ＝.

[答案]　

6．(2007·浙江卷)要在边长为16米的正方形草坪上安装喷水龙头，使整个草坪都能喷洒到水．假设每个喷水龙头的喷洒范围都是半径为6米的圆面，则需安装这种喷水龙头的个数最少是

(　)

A．3　　　　　 B．4 　　　　　　　　　　　　 C．5　　　　　　　　　 D．6

[解析]　一个喷水龙头所能覆盖的范围是直径为12米的圆面，该圆的内接面积最大的矩形是边长为6＝8.484的正方形，因此，边长为16的正方形至少需要4个这样的圆来全覆盖．选B.

[答案]　B

5．(2007·湖北卷)已知直线+＝1(a，b是非零常数)与圆x²+y²＝100有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有

(　)

A．60条　　　　　　　　　 B．66条

C．72条　 　　　　　　　　　　　　　　　　 D．78条

[解析]　圆x²+y²＝100上共有12个整数点对，即(10,0)，(－10,0)，(0,10)，(0，－10)，(6,8)，(－6,8)，(6，－8)，(－6，－8)，(8,6)，(8，－6)，(－8,6)，(－8，－6)．过这12个点中的两个点的直线共有C＝66条．其中与坐标轴平行的直线以及坐标轴在内的10条直线不符合题意．(－8，－6)与(8,6)，(－8,6)与(8，－6)，(－6，－8)与(6,8)，(－6,8)与(6，－8)这四组点关于原点对称，由它们组成的直线过原点，与题意不符．与圆相切的直线共有8条满足题意，故共有C－10－4+8＝60条直线满足题意，选A.

[答案]　A

4．设a，b，c是互不相等的正数，则下列等式中不恒成立的是

(　)

A．|a－b|≤|a－c|+|b－c|

B．a²+≥a+

C．|a－b|+≥2

D.－≤－

[解析]　对于选项(A)：|a－b|＝|(a－c)－(b－c)|≤|a－c|+|b－c|恒成立

对于选项(B)：(a²+)－(a+)＝(a+)²－(a+)－2＝(a+－2)(a++1)

＝≥0恒成立

对于选项(D)：－≤－⇔≤⇔+≥+，显然此式恒成立．

对于选项(C)：当a＞b时，|a－b|+≥2成立；当a＜b时，如a＝1，b＝2得|a－b|+＝0，即|a－b|+≥2不恒成立．故选C.

[答案]　C

3．用反证法证明命题“三角形的三个内角中至少有一个不大于60°”时，反设正确的是

(　)

A．假设三内角都不大于60°

B．假设三内角都大于60°

C．假设三内角至多有一个大于60°

D．假设三内角至多有两个大于60°

[答案]　B

2．(2009·山东卷理)设P是△ABC所在平面内的一点，+＝2，则

(　)

A.+＝0　 　　　　　　　　　　　　　 B.+＝0

C.+＝0　 　　　　　　　　　　　　　 D.++＝0

[解析]　因为+＝2，所以点P为线段AC的中点，所以应该选B.

[答案]　B

1．(2009·广东卷理)给定下列四个命题：

①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；

②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；

③垂直于同一直线的两条直线相互平行；

④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．

其中，为真命题的是

(　)

A．①和②　　　　　　 B．②和③

C．③和④　 　　　　　　　　　　　　　　 D．②和④

[答案]　D

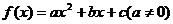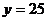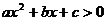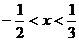11．已知二次函数的图象与直线有公共点，且不等式的解集是，求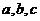的取值范围；

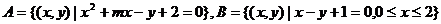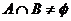10．已知集合，若,求实数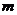的取值范围