
5.依次填入下列横线处的词语,最恰当的一组是
①其实作为军队作家都有一种难以 的情结,军事生活总是让他们那样魂绕梦牵。
②西方文化与东方传统在上海碰撞,新旧事物相互 ,缔造出上海独特的“海派文化”。
③一些医生受效益驱动,私开处方,抬高药价, 损害了患者的根本利益。 这些医生名气有多大,也要把他们从医院清理出去。
A.消释 交融 因而/不管 B.消失 交织 进而/不管
C.消释 交融 因而/尽管 D.消失 交织 进而/尽管
4.下列各项中各句诗歌全部符合原文的一项是
A. 阴阴夏木转黄鹂 渌水荡漾清猿啼 贾生才调更无论
B. 风紧角弓鸣 野旷天低树 罟师荡桨向临圻
C. 海上升明月 清辉玉臂寒 何时倚虚幌
D. 唯有牡丹真国色 分曹射覆蜡灯红 无那金闺万里愁
3.下列词语,没有错别字的一组是
A.厮打 闭门羹 味同嚼腊 生死攸关 B.告罄 挖墙脚 通宵达旦 出谋画策
C.疏浚 座右铭 竭泽而渔 万念俱灰 D.清冽 没辙儿 不修边辐 靡靡之音
2.下列各组词语中,加点的字读音完全相同的一组是
A.累及 磊落 护苗保蕾 身陷缧绁 B.栖息 蹊跷 芳草萋萋 休戚相关
C.瑰丽 日晷 大家闺秀 奉为圭臬 D.悔悟 晦涩 诲人不倦 毁誉参半
1.下列词语加点字的读音,完全相同的一组是
A.胸脯 俯瞰 抚育 釜底抽薪 辅车相依 B.咀嚼 绝招 角斗 一觉醒来 倔头倔脑
C.梦魇 俨然 掩饰 偃旗息鼓 广衍沃野 D.脊梁 贫瘠 给予 济济一堂 刀枪剑戟
18、(安徽06卷)证明(Ⅰ)令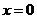 ,则
,则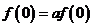 ,∵
,∵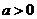 ,∴
,∴ 。
。
(Ⅱ)①令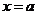 ,∵
,∵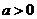 ,∴
,∴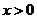 ,则
,则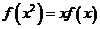 。
。
假设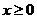 时,
时,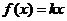
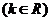 ,则
,则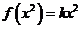 ,而
,而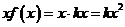 ,∴
,∴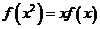 ,即
,即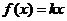 成立。
成立。
②令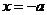 ,∵
,∵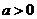 ,∴
,∴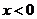 ,
,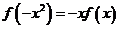
假设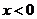 时,
时,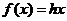
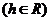 ,则
,则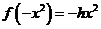 ,而
,而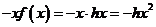 ,∴
,∴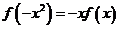 ,即
,即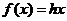 成立。∴
成立。∴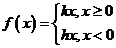 成立。
成立。
(Ⅲ)当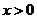 时,
时,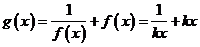 ,
,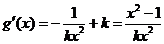
令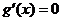 ,得
,得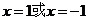 ;
;
当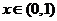 时,
时,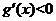 ,∴
,∴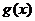 是单调递减函数;
是单调递减函数;
当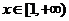 时,
时,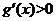 ,∴
,∴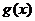 是单调递增函数;
是单调递增函数;
所以当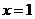 时,函数
时,函数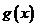 在
在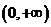 内取得极小值,极小值为
内取得极小值,极小值为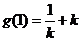
17.(安徽07卷)本小题主要考查函数导数的概念与计算,利用导数研究函数的单调性、极值和证明不等式的方法,考查综合运用有关知识解决问题的能力.本小题满分14分.
(Ⅰ)解:根据求导法则有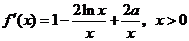 ,
,
故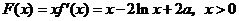 ,
,
于是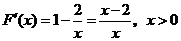 ,
,
列表如下:
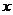 |
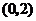 |
2 |
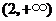 |
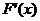 |
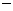 |
0 |
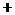 |
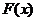 |
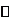 |
极小值 |
 |
故知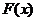 在
在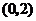 内是减函数,在
内是减函数,在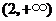 内是增函数,所以,在
内是增函数,所以,在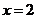 处取得极小值
处取得极小值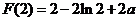 .
.
(Ⅱ)证明:由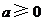 知,
知,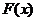 的极小值
的极小值 .
.
于是由上表知,对一切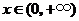 ,恒有
,恒有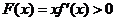 .
.
从而当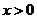 时,恒有
时,恒有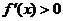 ,故
,故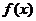 在
在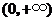 内单调增加.
内单调增加.
所以当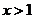 时,
时,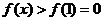 ,即
,即 .
.
故当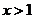 时,恒有
时,恒有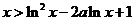 .
.
16、(安徽06卷)(1) 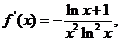 若
若 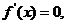 则
则 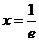 列表如下
列表如下
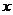 |
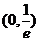 |
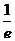 |
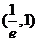 |
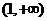 |
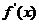 |
+ |
0 |
- |
- |
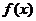 |
单调增 |
极大值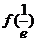 |
单调减 |
单调减 |
(2) 在 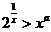 两边取对数, 得
两边取对数, 得 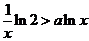 ,由于
,由于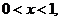 所以
所以
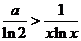 (1)
(1)
由(1)的结果可知,当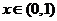 时,
时, 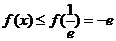 ,
,
为使(1)式对所有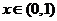 成立,当且仅当
成立,当且仅当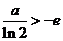 ,即
,即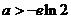
18、(安徽06卷)已知函数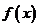 在R上有定义,对任何实数
在R上有定义,对任何实数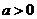 和任何实数
和任何实数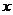 ,
,
都有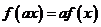
(Ⅰ)证明 ;
;
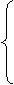
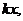
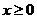 ,
,
(Ⅱ)证明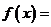 其中
其中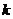 和
和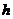 均为常数;
均为常数;
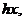
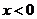 ,
,
(Ⅲ)当(Ⅱ)中的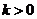 时,设
时,设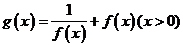 ,讨论
,讨论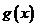 在
在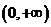 内的单调性并求极值。
内的单调性并求极值。
(16).(安徽08卷)设函数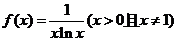
(Ⅰ)求函数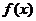 的单调区间;
的单调区间;
(Ⅱ)已知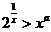 对任意
对任意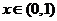 成立,求实数
成立,求实数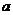 的取值范围。
的取值范围。
17.(安徽07卷) 设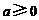 ,
,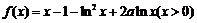 .
.
(Ⅰ)令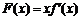 ,讨论
,讨论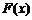 在
在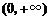 内的单调性并求极值;
内的单调性并求极值;
(Ⅱ)求证:当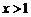 时,恒有
时,恒有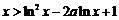 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com