
8.(2009·陕西高考)“m>n>0”是“方程mx2+ny2=1表示焦点在y轴上的椭圆”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解析:把椭圆方程化成+=1.若m>n>0,
则>>0.所以椭圆的焦点在y轴上.
反之,若椭圆的焦点在y轴上,
则>>0即有m>n>0.
答案:C
7.“sinα=”是“cos2α=”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
解析:充分性:如果sinα=,则cos2α=1-2sin2α=,成立;必要性:如果cos2α=,则sinα=±,不成立,可知是充分而不必要条件.
答案:A
6.(2009·安徽高考)“a+c>b+d”是“a>b且c>d”的 ( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
解析:“a+c>b+d” “a>b且c>d”,∴充分性不成立;“a>b且c>d”⇒“a+c>b+d”,∴必要性成立.
“a>b且c>d”,∴充分性不成立;“a>b且c>d”⇒“a+c>b+d”,∴必要性成立.
答案:A
5.(文)给定下列命题:
①若k>0,则方程x2+2x-k=0有实数根;
②“若a>b,则a+c>b+c”的否命题;
③“矩形的对角线相等”的逆命题;
④“若xy=0,则x、y中至少有一个为0”的否命题.
其中真命题的序号是 .
解析:①∵Δ=4-4(-k)=4+4k>0,
∴①是真命题.
②否命题:“若a≤b,则a+c≤b+c”是真命题.
③逆命题:“对角线相等的四边形是矩形”是假命题.
④否命题:“若xy≠0,则x、y都不为零”是真命题.
答案:①②④
(理)(2009·安徽高考)对于四面体ABCD,下列命题正确的是 (写出所有正确命题的编号).
①相对棱AB与CD所在的直线是异面直线;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高的垂足重合;
④任何三个面的面积之和都大于第四个面的面积;
⑤分别作三组相对棱中点的连线,所得的三条线段相交于一点.
 解析:①正确,∵A、B、C、D四点不共面,∴AB与CD异面;
解析:①正确,∵A、B、C、D四点不共面,∴AB与CD异面;
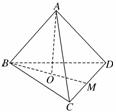
②不正确,如图,
若A在底面BCD的射影O是△BCD的三条高线交点,那么延长BO交CD于M,则BM⊥CD,可证CD⊥面ABM.
那么CD⊥AB,即四面体相对棱异面垂直,而一般四面体ABCD相对棱不一定垂直,∴②不正确;
③不正确,如图,
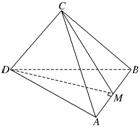 作DM⊥AB于M,连结CM,
作DM⊥AB于M,连结CM,
假设CM⊥AB,
那么AB⊥面CMD.
又CD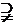 面CMD,
面CMD,
∴AB⊥CD.
而CD与AB不一定垂直,
∴③不正确;④显然成立;
⑤如图,取各棱中点M、N、P、Q、S、T,
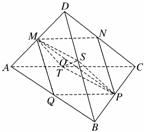
∴▱MNPQ的对角线MP与NQ交于一点O.
同理▱MSPT的对角线MP与ST也交于点O,
∴三条线MP、NQ、ST交于一点O.
答案:①④⑤
|
题组二 |
充分条件必要条件的判定 |
4.有下列四个命题,其中真命题有:
①“若x+y=0,则x、y互为相反数”的逆命题;
②“全等三角形的面积相等”的否命题;
③“若q≤1,则x2+2x+q=0有实根”的逆命题;
④“不等边三角形的三个内角相等”的逆否命题.
其中真命题的序号为 ( )
A.①② B.②③ C.①③ D.③④
解析:命题①的逆命题:“若x、y互为相反数,则x+y=0”是真命题;命题②可考虑其逆命题“面积相等的三角形是全等三角形”是假命题,因此命题②的否命题是假命题;命题③的逆命题:“若x2+2x+q=0有实根,则q≤1”是真命题;命题④是假命题.
答案:C
3.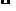 已知命题p:∃x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2},下列结论:①命题“p∧q”是真命题; ②命题“p∧ q”是假命题;
已知命题p:∃x∈R,使tanx=1,命题q:x2-3x+2<0的解集是{x|1<x<2},下列结论:①命题“p∧q”是真命题; ②命题“p∧ q”是假命题;
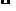
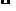
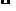 ③命题“ p∨q”是真命题; ④命题“ p∨ q”是假命题.
③命题“ p∨q”是真命题; ④命题“ p∨ q”是假命题.
其中正确的是 ( )
A.②③ B.①②④ C.①③④ D.①②③④
 解析:命题p:∃x∈R,使tanx=1正确,命题q:x2-3x+2<0的解集是{x|1<x<2}也正确,∴①命题“p∧q”是真命题;②命题“p∧ q”是假命题;③命题“ p∨ q”是真命题;④命题“ p∨ q”是假命题.
解析:命题p:∃x∈R,使tanx=1正确,命题q:x2-3x+2<0的解集是{x|1<x<2}也正确,∴①命题“p∧q”是真命题;②命题“p∧ q”是假命题;③命题“ p∨ q”是真命题;④命题“ p∨ q”是假命题.
答案:D
2.(2009·重庆高考)命题“若一个数是负数,则它的平方是正数”的逆命题是 ( )
A.“若一个数是负数,则它的平方不是正数”
B.“若一个数的平方是正数,则它是负数”
C.“若一个数不是负数,则它的平方不是正数”
D.“若一个数的平方不是正数,则它不是负数”
解析:结论与条件互换位置选B.
答案:B
1.原命题:“设a、b、c∈R,若ac2>bc2,则a>b”的逆命题、否命题、逆否命题中真命题共有 ( )
A.0个 B.1个 C.2个 D.3个
解析:由题意可知,原命题正确,逆命题错误,所以否命题错误,而逆否命题正确.
答案:B
3.A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验,每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率为,服用B有效的概率为.
(1)求一个试验组为甲类组的概率;
(2)观察3个试验组,用ξ表示这3个试验组中甲类组的个数.求ξ的分布列和数学期望.
解答:(1)设Ai表示事件“一个试验组中,服用A有效的小白鼠有i只”,
i=0,1,2,
Bi表示事件“一个试验组中,服用B有效的小白鼠有i只”,i=0,1,2.
依题意有P(A1)=2××=,P(A2)=×=,P(B0)=×=,
P(B1)=2××=.
所求的概率为P=P(B0·A1)+P(B0·A2)+P(B1·A2)
=×+×+×=.
(2)ξ的可能值为0,1,2,3且ξ-B.
P(ξ=0)=3=,P(ξ=1)=C××2=,
P(ξ=2)=C×2×=,P(ξ=3)=3=.
ξ的分布为
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
数学期望Eξ=3×=.
2.若随机变量X的概率分布密度函数是φμ,σ(x)=e-,(x∈R),则E(2X-1)=________.
解析:σ=2,μ=-2,E(2X-1)=2E(X)-1=2×(-2)-1=-5.
答案:-5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com