
2.求下列函数的定义域:
(1)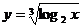 (2)
(2)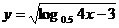
解:由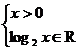 得x>0
得x>0
∴所求函数定义域为:{x|x>0}
(2)由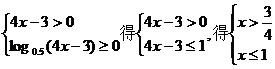 即
即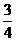 <x≤1
<x≤1
∴所求函数定义域为{x|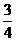 <x≤1
<x≤1
1.求下列函数的反函数:
(1)y=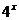 (x∈R)
(2)y=
(x∈R)
(2)y=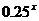 (x∈R)
(x∈R)
(3)y=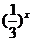 (x∈R)
(4)y=
(x∈R)
(4)y=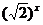 (x∈R)
(x∈R)
(5)y=lgx(x>0)
(6)y=2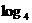 x(x>0)
x(x>0)
(7)y=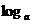 (2x)(a>0,且a≠1,x>0) (8)y=
(2x)(a>0,且a≠1,x>0) (8)y=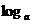
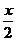 (a>0,a≠1,x>0)
(a>0,a≠1,x>0)
解:(1)所求反函数为:y=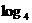 x(x>0)
x(x>0)
(2)所求反函数为:y=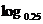 x(x>0)
x(x>0)
(3)所求反函数为:y=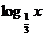 (x>0)
(x>0)
(4)所求反函数为:y=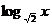 (x>0)
(x>0)
(5)所求反函数为:y=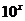 (x∈R)
(x∈R)
(6)所求反函数为:y=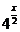 =
=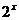 (x∈R)?
(x∈R)?
(7)所求反函数为:y=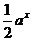 (a>0,且a≠1,x∈R)?
(a>0,且a≠1,x∈R)?
(8)所求反函数为:y=2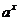 (a>0,且a≠1,x∈R)?
(a>0,且a≠1,x∈R)?
⑴对数的定义, ⑵指数式与对数式互换 ⑶求对数式的值
2.求下列函数的定义域:
(1)y=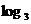 (1-x)
(2)y=
(1-x)
(2)y=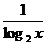
(3)y=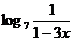
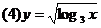
解:(1)由1-x>0得x<1 ∴所求函数定义域为{x|x<1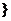
(2)由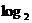 x≠0,得x≠1,又x>0 ∴所求函数定义域为{x|x>0且x≠1}
x≠0,得x≠1,又x>0 ∴所求函数定义域为{x|x>0且x≠1}
(3)由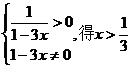 ∴所求函数定义域为{x|x<
∴所求函数定义域为{x|x<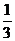
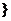
(4)由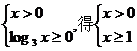 ∴x≥1 ∴所求函数定义域为{x|x≥1}
∴x≥1 ∴所求函数定义域为{x|x≥1}
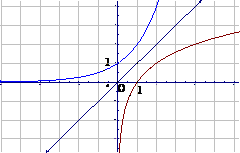
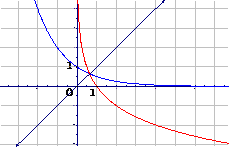
1.画出函数y=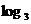 x及y=
x及y=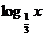 的图象,并且说明这两个函数的相同性质和不同性质.
的图象,并且说明这两个函数的相同性质和不同性质.
解:相同性质:两图象都位于y轴右方,都经过点(1,0),这说明两函数的定义域都是(0,+∞),且当x=1,y=0.
不同性质:y=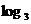 x的图象是上升的曲线,y=
x的图象是上升的曲线,y=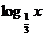 的图象是下降的曲线,这说明前者在(0,+∞)上是增函数,后者在(0,+∞)上是减函数.
的图象是下降的曲线,这说明前者在(0,+∞)上是增函数,后者在(0,+∞)上是减函数.
例1(课本第94页)求下列函数的定义域:
(1)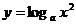 ;
(2)
;
(2)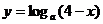 ;
(3)
;
(3)
分析:此题主要利用对数函数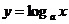 的定义域(0,+∞)求解
的定义域(0,+∞)求解
解:(1)由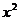 >0得
>0得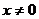 ,∴函数
,∴函数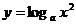 的定义域是
的定义域是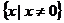 ;
;
(2)由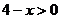 得
得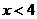 ,∴函数
,∴函数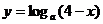 的定义域是
的定义域是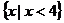
(3)由9-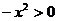 得-3
得-3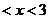 ,
,
∴函数 的定义域是
的定义域是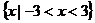
例2求下列函数的反函数
①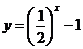 ②
②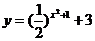
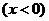
解:① 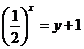 ∴
∴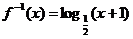
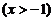
② 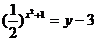 ∴
∴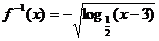
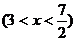
3.对数函数的性质
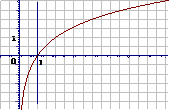
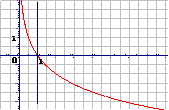
由对数函数的图象,观察得出对数函数的性质见P87 表
|
|
a>1 |
0<a<1 |
|
图 象 |
 |
 |
|
性 质 |
定义域:(0,+∞) |
|
|
值域:R |
||
|
过点(1,0),即当x=1时,y=0 |
||
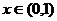 时 时 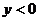 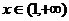 时 时  |
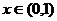 时 时  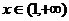 时 时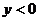 |
|
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
2.对数函数的图象
由于对数函数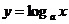 与指数函数
与指数函数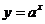 互为反函数,所以
互为反函数,所以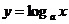 的图象与
的图象与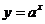 的图象关于直线
的图象关于直线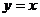 对称因此,我们只要画出和
对称因此,我们只要画出和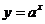 的图象关于
的图象关于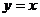 对称的曲线,就可以得到
对称的曲线,就可以得到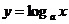 的图象,然后根据图象特征得出对数函数的性质
的图象,然后根据图象特征得出对数函数的性质
1.对数函数的定义:
函数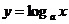
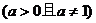 叫做对数函数;它是指数函数
叫做对数函数;它是指数函数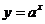
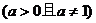 的反函数
的反函数
对数函数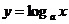
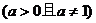 的定义域为
的定义域为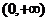 ,值域为
,值域为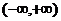
3、我们研究指数函数时,曾经讨论过细胞分裂问题,某种细胞分裂时,得到的细胞的个数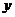 是分裂次数
是分裂次数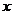 的函数,这个函数可以用指数函数
的函数,这个函数可以用指数函数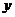 =
=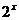 表示
表示
现在,我们来研究相反的问题,如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数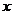 就是要得到的细胞个数
就是要得到的细胞个数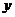 的函数根据对数的定义,这个函数可以写成对数的形式就是
的函数根据对数的定义,这个函数可以写成对数的形式就是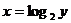
如果用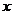 表示自变量,
表示自变量,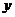 表示函数,这个函数就是
表示函数,这个函数就是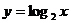
由反函数概念可知, 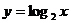 与指数函数
与指数函数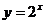 互为反函数
互为反函数
这一节,我们来研究指数函数的反函数对数函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com