
19、 设函数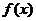 的定义域是
的定义域是 ,对于任意正实数
,对于任意正实数 恒有
恒有
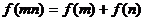 ,且当
,且当 时,
时,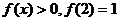 。
。
(1)求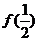 的值;
的值;
(2)求证: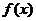 在
在 上是增函数;
上是增函数;
(3)求方程 的根的个数。
的根的个数。
18. 若椭圆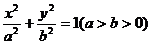 过点(-3,2),离心率为
过点(-3,2),离心率为 ,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为 ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B。
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B。
(1)求椭圆的方程;
(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的方程;
(3)求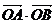 的最大值与最小值。
的最大值与最小值。
17. 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
16、 设集合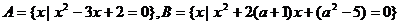
(1)若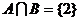 ,求实数
,求实数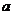 的值;
的值;
(2)若 ,求实数
,求实数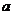 的取值范围;
的取值范围;
(3)若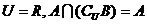 ,求实数
,求实数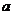 的取值范围。
的取值范围。
15、
已知O为原点,向量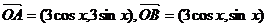 ,
,
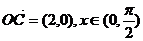 。
。
(1)求证: ;
;
(2)求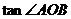 的最大值及相应的
的最大值及相应的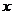 值;
值;
14.
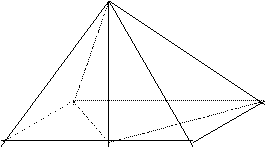
 如图在四棱锥P-ABCD中,O为CD上的动点,四边形ABCD满足条件
如图在四棱锥P-ABCD中,O为CD上的动点,四边形ABCD满足条件
|
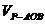 恒为定值(写上你认为正确的一个条件即可)。
恒为定值(写上你认为正确的一个条件即可)。
|
|
|
|
|
13. 在空间,下列命题正确的是
在空间,下列命题正确的是
 (注意:把你认为正确的都填上)。
(注意:把你认为正确的都填上)。
①
如果两条直线a、b分别与直线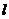 平行,那么
平行,那么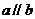 ;
;
②
如果直线a与平面 内的一条直线b平行,那么
内的一条直线b平行,那么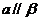 ;
;
③
如果直线a与平面 内的两条直线b、c都垂直,那么
内的两条直线b、c都垂直,那么 ;
;
④
如果平面 内的一条直线a垂直于平面
内的一条直线a垂直于平面 ,那么
,那么 。
。
12.已知a、b、c、d是四条互不重合的直线,且c、d分别为a、b在平面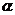 上的射影。给出下面两组判断:第一组:1
上的射影。给出下面两组判断:第一组:1 2
2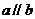 ;第二组:3
;第二组:3 4
4 。分别从两组中各选一个论断,使之一个作条件,另一个作结论,写出一个正确的命题
。分别从两组中各选一个论断,使之一个作条件,另一个作结论,写出一个正确的命题


11.三棱锥P-ABC中,PA、PB、PC两两垂直,且PA+PB=4,PC=1,则此三棱锥的体积( )
(A)
有最大值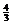 ,无最小值;
(B) 有最小值
,无最小值;
(B) 有最小值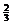 ,无最大值;
,无最大值;
(C)
有最大值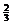 ,无最小值;
(D) 无最大值,也无最小值;
,无最小值;
(D) 无最大值,也无最小值;
10.斜三棱柱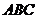 --
--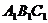 中,
中, 则
则 在底面
在底面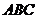 上的射影
上的射影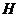 必在( )
必在( )
(A) 直线AB上 (B) 直线BC上
(C) 直线CA上 (D) △ABC内部
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com