1. 2009年10月，诺贝尔化学奖得主Venkatruaman Ramakrishnan、Thomas Steitz和Ada Yonath三位科学家都采用了X射线蛋白质晶体学的技术，标识出了构成核糖体的成千上万个原子。这些科学家不仅让我们知晓了核糖体的“外貌”，而且在原子层上揭示了核糖体功能的机理。对于原子的概念叙述正确的是

　　　 A、不能再分的最小微粒　　　　　

　　　 B、保持物质化学性质的最小微粒

　　　 C、化学变化中不能再分的最小微粒

　　　 D、构成物质的最小微粒

22．(14分)

　(2009·北京东城模拟)如图17所示，四棱锥P－ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，且PA＝2，E为PD中点．

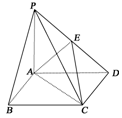
图17

　(1)求证：PA⊥平面ABCD；

(2)求二面角E－AC－D的大小；

(3)在线段BC上是否存在点F，使得点E到平面PAF的距离为？若存在，确定点F的位置；若不存在，请说明理由．

解：(1)证明：∵底面ABCD为正方形，∴BC⊥AB，又BC⊥PB，∴BC⊥平面PAB，∴BC⊥PA.

同理CD⊥PA，

∴PA⊥平面ABCD.

　(2)建立如图18所示的空间直角坐标系A－xyz，

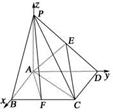
图18

则A(0,0,0)，C(2,2,0)、E(0,1,1)．

设m＝(x，y，z)为平面AEC的一个法向量．

则m⊥，m⊥.

又＝(0,1,1)，＝(2,2,0)，

∴

令x＝1，则y＝－1，z＝1，得m＝(1，－1,1)

又＝(0,0,2)是平面ACD的一个法向量，

设二面角E－AC－D的大小为θ，则

cosθ＝cos?m，?＝AP,\s\up6(→\s\up7(　＝＝.

∴二面角E－AC－D的大小为arccos.

(3)设F(2，t,0)(0≤t≤2)，n＝(a，b，c)为平面PAF的一个法向量，则n⊥，n⊥.

又＝(0,0,2)，＝(2，t,0)，∴

令a＝t，则b＝－2，c＝0，

得n＝(t，－2,0)．

又＝(0,1,1)．

∴点E到平面PAF的距离为＝，

∴＝，解得t＝1，即F(2,1,0)．

∴在线段BC上存在点F，且F为BC中点，使得点E到平面PAF的距离为.

21．(12分)(2009·唐山二模)如图15，已知三棱柱ABC－A₁B₁C₁的侧棱与底面所成的角为60°，AB＝BC，A₁A＝A₁C＝2，AB⊥BC，侧面AA₁C₁C⊥底面ABC.

(1)证明：A₁B⊥A₁C₁；

(2)求二面角A－CC₁－B的大小；

(3)求经过A₁、A、B、C四点的球的表面积．

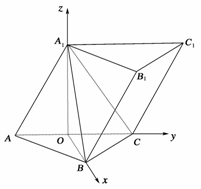
图15

图16

解：取AC中点为O，由A₁A＝A₁C，AB＝BC，知A₁O⊥AC，BO⊥AC，又平面AA₁C₁C⊥平面ABC，所以A₁O⊥OB.

建立如图16所示的坐标系O－xyz，则A(0，－1,0)，

B(1,0,0)，A₁(0,0，)，C(0,1,0)．

(1)∵＝(1,0，－)，＝＝(0,2,0)，

∴·＝0，∴A₁B⊥A₁C₁.

(2)设n＝(x，y，z)为面BCC₁的一个法向量．

∵＝(－1,1,0)，＝＝(0,1，)，

又n·＝n·＝0，

∴取n＝(，，－1)．

又m＝(1,0,0)是面ACC₁的法向量，

cos?m，n?＝＝＝.

由点B在平面ACC₁内的射影O在二面角的面ACC₁内，知二面角A－CC₁－B为锐角，

所以二面角A－CC₁－B的大小为arccos.

(3)设球心为O₁，因为O是△ABC的外心，A₁O⊥平面ABC，

所以点O₁在A₁O上，则O₁是正三角形A₁AC的中心．

则球半径R＝A₁A＝，球表面积S＝4πR²＝π.

20．(12分)在直三棱柱ABC－A₁B₁C₁中，AB₁⊥BC₁，AB＝CC₁＝a，BC＝b.

(1)设E，F分别为AB₁，BC₁的中点，求证：EF∥平面ABC；

(2)求证：A₁C₁⊥AB；

(3)求点B₁到平面ABC₁的距离．

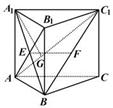
图14

解：(1)∵E，F分别为AB₁，BC₁的中点，∴EF∥A₁C₁.

∵A₁C₁∥AC，

∴EF∥AC，∴EF∥平面ABC.

(2)∵AB＝CC₁，∴AB＝BB₁.

又三棱柱为直三棱柱，

∴四边形ABB₁A₁为正方形，

连结A₁B，则A₁B⊥AB₁.

又∵AB₁⊥BC₁，∴AB₁⊥平面A₁BC₁，∴AB₁⊥A₁C₁.

又A₁C₁⊥AA₁，∴A₁C₁⊥平面A₁ABB₁，∴A₁C₁⊥AB.

(3)∵A₁B₁∥AB，∴A₁B₁∥平面ABC₁，

∴A₁到平面ABC₁的距离等于B₁到平面ABC₁的距离，过A₁作A₁G⊥AC₁于G.

∵AB⊥平面ACC₁A₁，∴AB⊥A₁G，

从而A₁G⊥平面ABC₁，故A₁G即为所求的距离，

求得A₁G＝.

19．(12分)(2009·湖北联考)如图13，长方体AC₁中，AB＝2，BC＝AA₁＝1.E、F、G分别为棱DD₁、D₁C₁、BC的中点．

(1)试在底面A₁B₁C₁D₁上找一点H，使EH∥平面FGB₁；

(2)求四面体EFGB₁的体积．

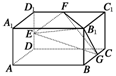
图13

解：(1)取A₁D₁的中点P，D₁P的中点H，连接DP、EH，则DP∥B₁G，EH∥DP，∴EH∥B₁G，又B₁G⊂平面FGB₁，∴EH∥平面FGB₁.

即H在A₁D₁上，且HD₁＝A₁D₁时，EH∥平面FGB₁.

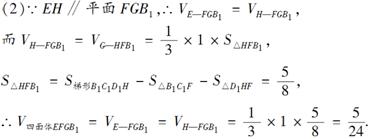
18．(12分)如图11，在△ABC中，AC＝BC＝1，∠ACB＝90°，点D在斜边AB上，∠BCD＝α(0<α<)．把△BCD沿CD折起到△B′CD的位置，使平面B′CD⊥平面ACD.

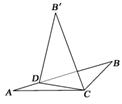
图11

　(1)求点B′到平面ACD的距离(用α表示)；

(2)当AD⊥B′C时，求三棱锥B′－ACD的体积．

解：(1)作B′E⊥CD于E.

∵平面B′CD⊥平面ACD，

∴B′E⊥平面ACD.

∴B′E的长为点B′到平面ACD的距离．

B′E＝B′C·sinα＝sinα.

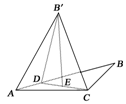
图12

　(2)∵B′E⊥平面ACD，

∴CE为B′C在平面ACD内的射影．

又AD⊥B′C，∴AD⊥CD(CE)．

∵AC＝BC＝1，∠ACB＝90°，

∴D为AB中点，且α＝.

∴S_△ACD＝·AC·BC＝，B′E＝sin＝.

∴V_B′－ACD＝··＝.

17．(12分)(2010·石家庄质检)如图10，在正方体ABCD－A₁B₁C₁D₁中，E、F分别为A₁B₁、A₁D₁的中点，G、H分别为BC、B₁D₁的中点．

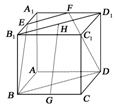
图10

　(1)指出直线GH与平面EFDB的位置关系，并加以证明；

(2)求异面直线GH与DF所成角的大小．

解：(1)连结EH，易知EH＝BG且EH∥BG，

所以四边形EHGB为平行四边形，所以GH∥BE，所以GH∥平面EFDB.

(2)取BD中点M，连结MF，易知MF∥BE，所以MF∥GH，

所以∠DFM为异面直线GH与DF所成的角，

设正方体棱长为2，

可得，MF＝，DF＝，MD＝，

在三角形MDF中，由余弦定理可得cos∠MFD＝，

∴异面直线GH与DF所成的角的大小为arccos.

16．(2010·东北三校一模)如图8，将∠B＝，边长为1的菱形ABCD沿对角线AC折成大小等于θ的二面角B-AC-D，若θ∈[，]，M、N分别为AC、BD的中点，则下面的四种说法：

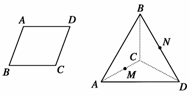
图8

①AC⊥MN；

②DM与平面ABC所成的角是θ；

③线段MN的最大值是，最小值是；

④当θ＝时，BC与AD所成的角等于.

其中正确的说法有__________(填上所有正确说法的序号)．

解析：如图9(1)，AC⊥BM，AC⊥MD⇒AC⊥平面BMD，所以AC⊥MN，①正确；因为θ∈[，]，且线与面所成角的范围为[0，]，所以DM与平面ABC所成的角不一定是θ，②错；BM＝DM＝，MN⊥BD，∠BMD＝θ，所以MN＝BM·cos＝·cos，所以线段MN的最大值是，最小值是，③正确；当θ＝时，过C作CE∥AD，连接DE(如图9(2))，且DE∥AC，则∠BCE(或补角)即为两直线的夹角，BM⊥DM，BM＝DM＝，BD²＝，又DE∥AC，则DE⊥平面BDM，∴DE⊥BD，BE²＝+1＝，cosBCE＝＝－≠0，所以④错．

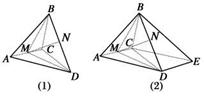
图9

答案：①③

15．如图7，∠BAD＝90°的等腰直角三角形ABD与正三角形CBD所在平面成60°的二面角，则AB与平面BCD所成角的大小为________．

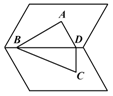
图7

解析：作AE⊥BD，连结CE，则CE⊥BD，∠AEC＝60°.

作AO⊥EC，则AO⊥面BCD，

连结BO，∠ABO即为AB与面BCD所成的角．

设AB＝a，则AE＝a，AO＝AEsin60°＝a×＝a.∴sin∠ABO＝＝.

∴∠ABO＝arcsin.

答案：arcsin

14．设球O的半径为R，A、B、C为球面上三点，A与B、A与C的球面距离为，B与C的球面距离为，则球O在二面角B－OA－C内的这部分球面的面积是__________．

解析：如图6所示．

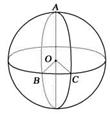
图6

∵A与B，A与C的球面距离都为，

∴OA⊥OB，OA⊥OC.

从而∠BOC为二面角B－OA－C的平面角．

又∵B与C的球面距离为，

∴∠BOC＝.

这样球O在二面角B－OA－C的部分球面的面积等于×4πR²＝R².

答案：R²