
21.(本小题满分13分)
设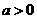 ,函数
,函数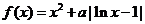
(1)当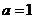 时,求曲线
时,求曲线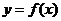 在
在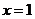 处的切
处的切 线方程;
线方程;
(2)当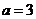 时,求函数
时,求函数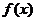 的单调性;
的单调性;
(3)当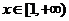 时,求函数
时,求函数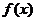 的最小值。
的最小值。
1-5 ACBBA 6-8DCB
20.(本小题满分13分)
已知圆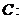
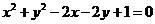 ,直线
,直线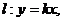 且
且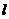 与圆
与圆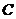 相交于
相交于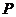 、
、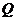 两点,点
两点,点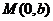 ,且
,且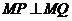 。
。
(1)当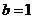 时,求
时,求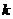 的值;
的值;
(2)当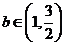 ,求
,求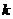 的取值范围。
的取值范围。
19.(本小题满分13分)
据调查,某地区100万从事传统农业的农民,人均年收入3000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农民产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有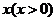 万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高2
万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高2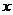 %,而进入企业工作的农民的人均收入为
%,而进入企业工作的农民的人均收入为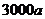 元(
元(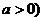 。
。
(1)在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工建立前的农民的年总收入,试求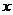 的取值范围;
的取值范围;
(2)在(1)的条件下,当地政府应该如何引导农 民(即
民(即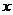 多大时),能使这1
多大时),能使这1 00万农民的人均年收入达到最大。
00万农民的人均年收入达到最大。
18.(本小题满分12分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是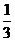 ,遇到红灯时停留的时间都是2min。
,遇到红灯时停留的时间都是2min。
(1)求这名学生在上学路上到第三个路口时首次遇到 红灯的概率;
红灯的概率;
(2)求这名学生在途中至少遇到一次红灯的概率;
(3)求这名学生在上学路上因遇到红灯停留的总时间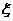 的分布列及期望。
的分布列及期望。
17.(本小题满分12分)
已知函数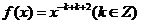 ,且
,且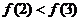 。
。
(1)求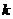 的值;
的值;
(2)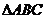 中,
中,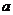 、
、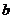 、
、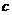 分别是角
分别是角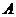 、
、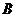 、
、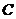 的对边,已知
的对边,已知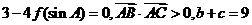 ,
,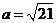 ,求
,求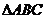 的面积。
的面积。
16.(本小题满分12分)
已知数列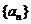 的前
的前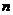 项和为
项和为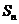 ,数列
,数列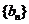 的前
的前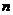 项和为
项和为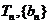 为等差数列且各项均为正数,
为等差数列且各项均为正数,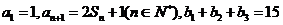
(1)求数列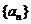 的通项公式;
的通项公式;
(2)若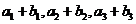 成等比数列,求
成等比数列,求
15.已知函数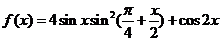
(I)设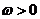 为常数,若
为常数,若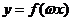 在区间
在区间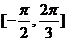 上是增函数,则
上是增函数,则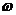 的取值范围是_____________。
的取值范围是_____________。
(II)若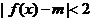 成立的充分条件是
成立的充分条件是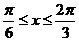 ,则实数
,则实数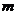 的取值范围是________
的取值范围是________ _。
_。
14.等某一等差数列的首项为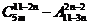 ,公差为
,公差为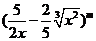 展开式的常数项,其中
展开式的常数项,其中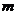 是
是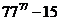 除以19的余数
除以19的余数 ,则比数列的前__________项和最大,最大值为____________。
,则比数列的前__________项和最大,最大值为____________。
13.在计算“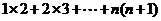 ”时,某同学学到了如下一种
”时,某同学学到了如下一种
方法:
先改写第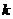 项:
项: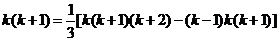 ,
,
由此得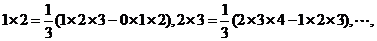
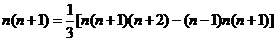
相加,得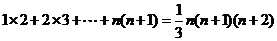
类比上述方法,请你 计算“
计算“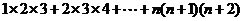 ”其,结果为______________________。
”其,结果为______________________。
12.如果直线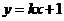 与圆
与圆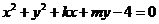 相交于
相交于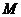 、
、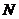
两点, 且点
且点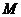 、
、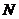 关于直线
关于直线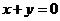 对称,则不等式组
对称,则不等式组
所表示的平面区域的面积为_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com