3.在平面直角坐标系中，将点P(-2,3)沿x轴方向向右平移3个单位得到点Q，则点Q的坐标是(　　　 )　 D

　 A.(-2,6)　　　　 B.(-2,0)　　　　 C.(-5,3)　　　　 D.(1,3)

2.某校乒乓球训练队共有9名队员，他们的年龄(单位：岁)分别为：12,13,13,14,12,13,15,13,15，则他们年龄的众数为(　　 ) B

　 A.12　　　　 B.13　　　　 C.14　　　　 D.15

1.-5的相反数是(　　　 )　 A

　 A.5　　　　　 B.-5　　　　 C.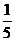　　　　 D.

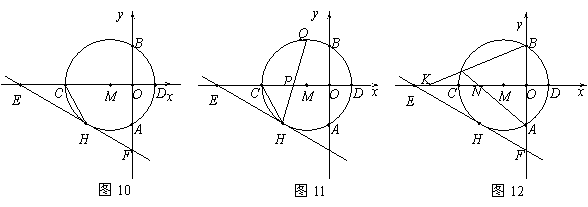
23．(本题9分)如图10，以点M(－1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－ x－ 与⊙M相切于点H，交x轴于点E，交y轴于点F．

　 (1)请直接写出OE、⊙M的半径r、CH的长；(3分)

(2)如图11，弦HQ交x轴于点P，且DP:PH＝3:2，求cos∠QHC的值；(3分)

(3)如图12，点K为线段EC上一动点(不与E、C重合)，连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．(3分)

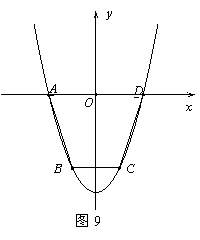
22．(本题9分)如图9，抛物线y＝ax²+c(a＞0)经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A(－2,0)，B(－1, －3)．

　 (1)求抛物线的解析式；(3分)

(2)点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；(2分)

(3)在第(2)问的结论下，抛物线上的点P使S_△PAD＝4S_△ABM成立，求点P的坐标．(4分)

21．(本题8分)儿童商场购进一批M型服装，销售时标价为75元/件，按8折销售仍可获利50%．商场现决定对M型服装开展促销活动，每件在8折的基础上再降价x元销售，已知每天销售数量y(件)与降价x元之间的函数关系为y＝20+4x(x＞0)

(1)求M型服装的进价；(3分)

(2)求促销期间每天销售M型服装所获得的利润W的最大值．(5分)

销售，已知每天销售数量与降价

20．(本题7分)如图8，△AOB和△COD均为等腰直角三角形，∠AOB＝∠COD＝90º，D在AB上．

(1)求证：△AOB≌△COD；(4分)

(2)若AD＝1，BD＝2，求CD的长．(3分)

19．(本题7分)低碳发展是今年深圳市政府工作报告提出的发展理念．近期，某区与某技术支持单位合作，组织策划了该区“低碳先锋行动”，开展低碳测量和排行活动．根据调查数据制作了频数分布直方图和扇形统计图，图6中从左到右各长方形的高度之比为2:8:9:7:3:1．

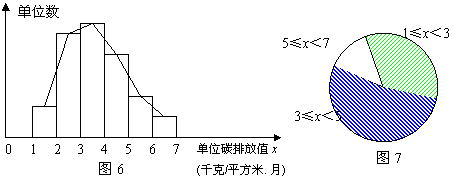
　 (1)已知碳排放值5≤x＜7(千克/平方米·月)的单位有16个，则此次行动调查了________个单位；(3分)

　 (2)在图7中，碳排放值5≤x＜7(千克/平方米·月)部分的圆心角为________度；(2分)

　 (3)小明把图6中碳排放值1≤x＜2的都看成1.5，碳排放值2≤x＜3的都看成2.5，以此类推，若每个被检单位的建筑面积均为10000平方米，则按小明的办法，可估算碳排放值x≥4(千克/平方米·月)的被检单位一个月的碳排放总值约为________________吨．(2分)

18．(本题6分)先化简分式÷－，然后在0，1，2，3中选一个你认为合适的a值，代入求值．

17．(本题6分)计算：( )^－2－2sin45º+ (π －3.14)⁰++(－1)³．