
1.-3的相反数是( )
A.3 B.-3 C. D.-
22.如图,平面直角坐标系中有一矩形ABCD(O为原点),点A、C分别在x轴、y轴上,且C点坐标为(0,6);将BCD沿BD折叠(D点在OC边上),使C点落在OA边的E点上,并将BAE沿BE折叠,恰好使点A落在BD的点F上.
(1)直接写出∠ABE、∠CBD的度数,并求折痕BD所在直线的函数解析式;
(2)过F点作FG⊥x轴,垂足为G,FG的中点为H,若抛物线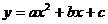 经过B、H、D三点,求抛物线的函数解析式;
经过B、H、D三点,求抛物线的函数解析式;
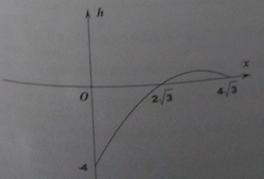
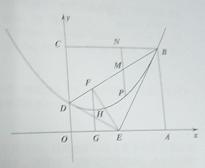 (3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PM<NM、PM=MN、PM>MN成立的x的取值范围。
(3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PM<NM、PM=MN、PM>MN成立的x的取值范围。
解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=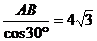
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(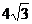 ,6) D(0,2)
,6) D(0,2)
设BD所在直线的函数解析式是y=kx+b
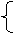
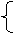
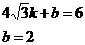 ∴
∴ 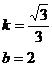
所以BD所在直线的函数解析式是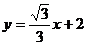
(2)∵EF=EA=ABtan30°=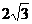 ∠FEG=180°-∠FEB-∠AEB=60°
∠FEG=180°-∠FEB-∠AEB=60°
又∵FG⊥OA
∴FG=EFsin60°=3 GE=EFcos60°=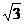 OG=OA-AE-GE=
OG=OA-AE-GE=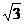
又H为FG中点
∴H(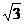 ,
,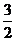 )
…………4分
)
…………4分
∵B(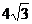 ,6) 、 D(0,2)、 H(
,6) 、 D(0,2)、 H(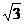 ,
,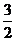 )在抛物线
)在抛物线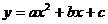 图象上
图象上
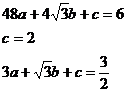 ∴
∴ 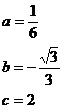
∴抛物线的解析式是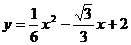
(2)∵MP=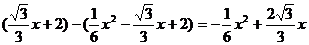
 MN=6-
MN=6-
H=MP-MN=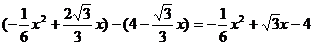
由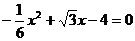 得
得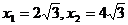
该函数简图如图所示:
当0<x<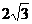 时,h<0,即HP<MN
时,h<0,即HP<MN
当x=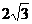 时,h=0,即HP=MN
时,h=0,即HP=MN
当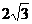 <x<
<x<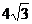 时,h>0,即HP>MN
时,h>0,即HP>MN
21.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连结PA、PB、PC、PD.
(1)当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并证明;
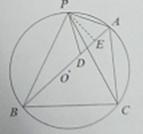 (2)若cos∠PCB=
(2)若cos∠PCB=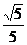 ,求PA的长.
,求PA的长.
解:(1)当BD=AC=4时,△PAD是以AD为底边的等腰三角形
∵P是优弧BAC的中点 ∴弧PB=弧PC
∴PB=PC
∵BD=AC=4 ∠PBD=∠PCA
∴△PBD≌△PCA
∴PA=PD 即△PAD是以AD为底边的等腰三角形
(2)由(1)可知,当BD=4时,PD=PA,AD=AB-BD=6-4=2
过点P作PE⊥AD于E,则AE=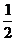 AD=1
AD=1
∵∠PCB=∠PAD
∴cos∠PAD=cos∠PCB=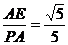
∴PA=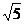
20.今年春季,我国云南、贵州等西南地区遇到多少不遇旱灾,“一方有难,八方支援”,为及时灌溉农田,丰收农机公司决定支援上坪村甲、乙、丙三种不同功率柴油发电机共10台(每种至少一台)及配套相同型号抽水机4台、3台、2台,每台抽水机每小时可抽水灌溉农田1亩.现要求所有柴油发电机及配套抽水机同时工作一小时,灌溉农田32亩.
(1)设甲种柴油发电机数量为x台,乙种柴油发电机数量为y台.
①用含x、y的式子表示丙种柴油发电机的数量;
②求出y与x的函数关系式;
(2)已知甲、乙、丙柴油发电机每台每小时费用分别为130元、120元、100元,应如何安排三种柴油发电机的数量,既能按要求抽水灌溉,同时柴油发电机总费用W最少?
解:(1)①丙种柴油发电机的数量为10-x-y
② ∵4x+3y+2(10-x-y)=32
∴y=12-2x
(2)丙种柴油发电机为10-x-y=(x-2)台
W=130x+120(12-2x)+100(x-2)
=-10x+1240
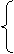 依题意解不等式组
依题意解不等式组 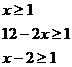 得:3≤x≤5.5
得:3≤x≤5.5
∵x为正整数 ∴x=3,4,5
∵W随x的增大而减少 ∴当x=5时 ,W最少为-10×5+1240=1190(元)
19.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,
连接DE,F为线段DE上一点,且∠AFE=∠B.
(1) 求证:△ADF∽△DEC
(2) 若AB=4,AD=3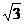 ,AE=3,求AF的长.
,AE=3,求AF的长.
(1)证明:∵四边形ABCD是平行四边形
∴AD∥BC AB∥CD
∴∠ADF=∠CED ∠B+∠C=180°
∵∠AFE+∠AFD=180 ∠AFE=∠B
∴∠AFD=∠C
∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形
∴AD∥BC CD=AB=4
又∵AE⊥BC ∴ AE⊥AD
在Rt△ADE中,DE=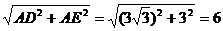
∵△ADF∽△DEC
∴ 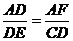 ∴
∴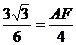 AF=
AF=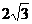
18.中央电视台举办的第14届“蓝色经典·天之蓝”杯青年歌手大奖赛,由部队文工团的A(海政)、B(空政)、C(武警)组成种子队,由部队文工团的D(解放军)和地方文工团的E(云南)、F(新疆)组成非种子队.现从种子队A、B、C与非种子队D、E、F中各抽取一个队进行首场比赛.
(1)请用适当方式写出首场比赛出场的两个队的所有可能情况(用代码A、B、C、D、E、F表示);
(2)求首场比赛出场的两个队都是部队文工团的概率P.
解:(1)由题意画树状图如下:
A B C








D E F D E F D E F
所有可能情况是:(A,D)、(A,E) 、(A,F) 、(B,D) 、(B,E) 、(B,F) 、(C,D) 、(C,E) 、(C,F)
(2)所有可能出场的等可能性结果有9个,其中首场比赛出场两个队都是部队文工团的结果有3个,
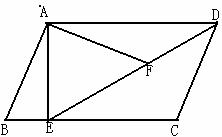 所以P(两个队都是部队文工团)=
所以P(两个队都是部队文工团)=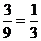
17.为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,依题意得
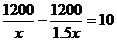
解得:x=40
经检验:x=40是原方程的根,所以1.5x=60
答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.
16.已知x1=-1是方程 的一个根,求m的值及方程的另一根x2。
的一个根,求m的值及方程的另一根x2。
解:由题意得: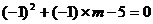 解得m=-4
解得m=-4
当m=-4时,方程为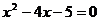
解得:x1=-1 x2=5
所以方程的另一根x2=5
15.如图,⊙O的半径等于1,弦AB和半径OC互相平分于点M.求扇形OACB的面积(结果保留π)
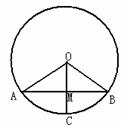 解:∵弦AB和半径OC互相平分
解:∵弦AB和半径OC互相平分
∴OC⊥AB
OM=MC=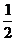 OC=
OC=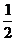 OA
OA
在Rt△OAM中,sinA=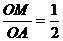
∴∠A=30°
又∵OA=OB ∴∠B=∠A=30° ∴∠AOB=120°
∴S扇形=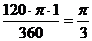
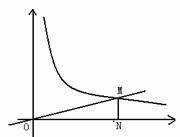
14.已知:正比例函数y=k1x的图象与反比例函数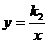 (x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,求这两个函数的解析式.
解:∵MN⊥x轴,点M(a,1)
∴S△OMN=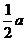 =2
=2
∴a=4
∴M(4,1)
 ∵正比例函数y=k1x的图象与反比例函数
∵正比例函数y=k1x的图象与反比例函数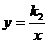 (x>0)的图象交于点M(4,1)
(x>0)的图象交于点M(4,1)
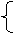
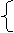 ∴
∴
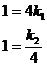 解得
解得
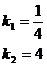
∴正比例函数的解析式是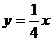 ,反比例函数的解析式是
,反比例函数的解析式是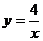
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com