
2. 掌握一些简单的条件概率的计算。
3、在一个盒子中有大小一样的20个球,其中10和红球,10个白球。求第1个人摸出1个红球,紧接着第2个人摸出1个白球的概率。
巩固练习: 课本55页练习1、2
课外作业:第60页 习题 2. 2 1 ,2 ,3
教学反思:1. 通过对具体情景的分析,了解条件概率的定义。
2、一个正方形被平均分成9个部分,向大正方形区域随机地投掷一个点(每次都能投中),设投中最左侧3个小正方形区域的事件记为A,投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B,求P(AB),P(A︱B)。
1、抛掷一颗质地均匀的骰子所得的样本空间为S={1,2,3,4,5,6},令事件A={2,3,5},B={1,2,4,5,6},求P(A),P(B),P(AB),P(A︱B)。
2.
P(·|B)的性质:
(1)非负性:对任意的A f.
f.
 ;
;
(2)规范性:P( |B)=1;
|B)=1;
(3)可列可加性:如果是两个互斥事件,则
 .
.
更一般地,对任意的一列两两部相容的事件 (I=1,2…),有
(I=1,2…),有
P  =
= .
.
例1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2 道题,求:
(l)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第 1 次抽到理科题的条件下,第2次抽到理科题的概率.
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
n( )=
)= =20.
=20.
根据分步乘法计数原理,n (A)=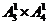 =12
.于是
=12
.于是
 .
.
(2)因为 n (AB)= =6
,所以
=6
,所以
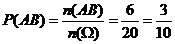 .
.
(3)解法 1 由( 1 ) ( 2 )可得,在第 1 次抽到理科题的条件下,第 2 次抽到理科题的概 .
.
解法2 因为 n (AB)=6 , n (A)=12 ,所以
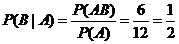 .
.
例2.一张储蓄卡的密码共位数字,每位数字都可从0-9中任选一个.某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过 2 次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率.
解:设第i次按对密码为事件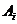 (i=1,2)
,则
(i=1,2)
,则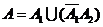 表示不超过2次就按对密码.
表示不超过2次就按对密码.
(1)因为事件 与事件
与事件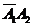 互斥,由概率的加法公式得
互斥,由概率的加法公式得
 .
.
(2)用B 表示最后一位按偶数的事件,则
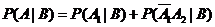
 .
.
课堂练习.
探究: 三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两名同学小.
若抽到中奖奖券用“Y ”表示,没有抽到用“
 ”,表示,那么三名同学的抽奖结果共有三种可能:Y
”,表示,那么三名同学的抽奖结果共有三种可能:Y
 ,
, Y
Y 和
和

 Y.用 B 表示事件“最后一名同学抽到中奖奖券” , 则 B 仅包含一个基本事件
Y.用 B 表示事件“最后一名同学抽到中奖奖券” , 则 B 仅包含一个基本事件
 Y.由古典概型计算公式可知,最后一名同学抽到中奖奖券的概率为
Y.由古典概型计算公式可知,最后一名同学抽到中奖奖券的概率为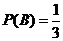 .
.
思考:如果已经知道第一名同学没有抽到中奖奖券,那么最后一名同学抽到奖券的概率又是多少?
因为已知第一名同学没有抽到中奖奖券,所以可能出现的基本事件只有
 Y和
Y和 Y
Y .而“最后一名同学抽到中奖奖券”包含的基本事件仍是
.而“最后一名同学抽到中奖奖券”包含的基本事件仍是
 Y.由古典概型计算公式可知.最后一名同学抽到中奖奖券的概率为
Y.由古典概型计算公式可知.最后一名同学抽到中奖奖券的概率为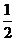 ,不妨记为P(B|A ) ,其中A表示事件“第一名同学没有抽到中奖奖券”.
,不妨记为P(B|A ) ,其中A表示事件“第一名同学没有抽到中奖奖券”.
已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
在这个问题中,知道第一名同学没有抽到中奖奖券,等价于知道事件 A 一定会发生,导致可能出现的基本事件必然在事件 A 中,从而影响事件 B 发生的概率,使得 P ( B|A )≠P ( B ) .
思考:对于上面的事件A和事件B,P ( B|A)与它们的概率有什么关系呢?
用 表示三名同学可能抽取的结果全体,则它由三个基本事件组成,即
表示三名同学可能抽取的结果全体,则它由三个基本事件组成,即 ={Y
={Y
 ,
,
 Y
Y ,
,
 Y}.既然已知事件A必然发生,那么只需在A={
Y}.既然已知事件A必然发生,那么只需在A={ Y
Y ,
,

 Y}的范围内考虑问题,即只有两个基本事件
Y}的范围内考虑问题,即只有两个基本事件 Y
Y 和
和
 Y.在事件 A 发生的情况下事件B发生,等价于事件 A 和事件 B 同时发生,即 AB 发生.而事件 AB 中仅含一个基本事件
Y.在事件 A 发生的情况下事件B发生,等价于事件 A 和事件 B 同时发生,即 AB 发生.而事件 AB 中仅含一个基本事件
 Y,因此
Y,因此
 =
=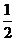 =
=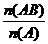 .
.
其中n ( A)和 n ( AB)分别表示事件 A 和事件 AB 所包含的基本事件个数.另一方面,根据古典概型的计算公式,

其中 n( )表示
)表示 中包含的基本事件个数.所以,
中包含的基本事件个数.所以,
 =
=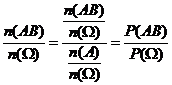 .
.
因此,可以通过事件A和事件AB的概率来表示P(B| A ) .
条件概率
1.定义
设A和B为两个事件,P(A)>0,那么,在“A已发生”的条件下,B发生的条件概率(conditional
probability ).  读作A 发生的条件下 B 发生的概率.
读作A 发生的条件下 B 发生的概率.
 定义为
定义为
 .
.
由这个定义可知,对任意两个事件A、B,若 ,则有
,则有
 .
.
并称上式微概率的乘法公式.
第二节:书面表达(满分25分)(试题内容见答题卡)
(暂缺)





第一节:短文改错(共10小题,每小题1分;满分10分)
此题要求改正所给短文中的错误。对标有题号的每一行做出判断:如无错误,在该行右边横线上画一个勾(√);如有错误(每行只有一个错误),则按下列情况改正:
该行多一个词:把多余的词用斜线(\)划掉,在该行右边横线上写出该词,并也用斜线划掉。
该行缺一个词:在缺词处加一个漏字符号(/\),在该行右边横线上写出该加的词。
该行错一个词:在错的词下划一横线,在该行右边横线上写出改正后的词。
注意:原行没有错的不要改。(试题内容见答题卡)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com