
5.(台州市2008学年第一学期高三年级期末质量评估试题数 学(理)
)
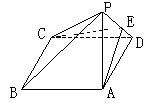
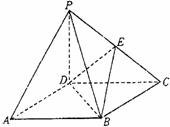 (本题满分15分)如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(本题满分15分)如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明PA//平面BDE;
(2)求二面角B-DE-C的平面角的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?
证明你的结论.
4.(1)证明:连接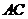 ,交
,交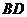 于
于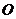 点,连接
点,连接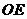 ,得
,得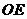 ∥
∥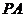 ,
,
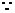
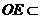 平面
平面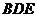 ,
,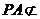 平面
平面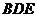 ,
,
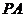 //平面
//平面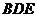 . ………………7分
. ………………7分
(2)  侧棱
侧棱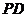 ⊥底面
⊥底面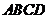 ,
, 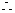
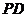 ⊥
⊥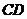 ,过
,过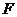 作
作 ⊥
⊥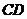 =
=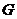 ,则
,则 ∥
∥ .
.
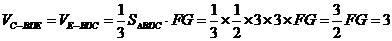 ,
,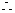
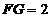 , ……12分
, ……12分
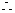 在棱
在棱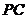 上存在点
上存在点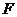 使三棱锥
使三棱锥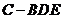 的体积为
的体积为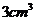 ,且
,且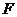 是线段
是线段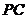 的三等分点.
的三等分点.
………………14分
4.台州市2008学年第一学期高三年级期末质量评估试题 数 学(文))
 (本小题满分14分)如图,四棱锥
(本小题满分14分)如图,四棱锥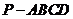 的底面
的底面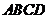 是正方形,侧棱
是正方形,侧棱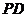 ⊥底面
⊥底面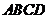 ,
,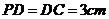 ,
,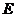 为
为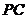 的中点.
的中点.
(1)证明: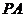 //平面
//平面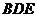 ;
;
(2)在棱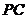 上是否存在点
上是否存在点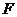 ,使三棱锥
,使三棱锥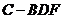 的
的
体积为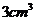 ?并说明理由.
?并说明理由.
2.(1)证明:依题意,该三视图所对应的直观图为一侧棱PA垂直于底面ABCD的四棱锥,且PA=AB=AD=1,四边形ABCD为正方形;
分别连结AC、BD交于O,连结EO,∵E是PD的中点,∴PB∥EO,
又PB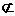 平面ACE,EO
平面ACE,EO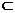 平面ACE,∴PB∥平面ACE。…………4分
平面ACE,∴PB∥平面ACE。…………4分
(2)证明:∵四边形ABCD是正方形,∴BD⊥AC,又PA⊥平面ABCD,
∴BD⊥PA,又∵PA∩AC=A,∴BD⊥平面PAC,
又PC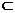 平面PAC,PC⊥BD。…………9分
平面PAC,PC⊥BD。…………9分 
(3)∵PA⊥平面ABCD,PA=AB=BC=1,∴VC-PAB=VP-ACD=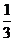 ×SΔABC×PA=
×SΔABC×PA=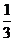 ×
×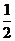 ×1×1×1=
×1×1×1=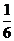 。∴三棱锥C-PAB的体积为
。∴三棱锥C-PAB的体积为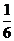 。…………14分
。…………14分
3(温州中学高三2008学年第一学期期末考试数 学 试 卷)
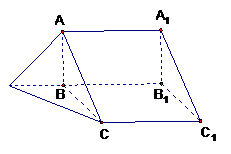 、(本题15分)如右放置在水平面上的组合体由直三棱柱
、(本题15分)如右放置在水平面上的组合体由直三棱柱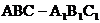 与正三棱锥
与正三棱锥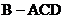 组成,其中,
组成,其中,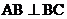 .它的正视图、俯视图、从左向右的侧视图的面积分别为
.它的正视图、俯视图、从左向右的侧视图的面积分别为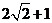 ,
,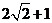 ,
,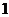 .
.
(Ⅰ)求直线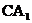 与平面
与平面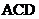 所成角的正弦;
所成角的正弦;
(Ⅱ)在线段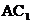 上是否存在点
上是否存在点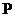 ,使
,使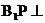 平面
平面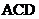 .若存在,确定点
.若存在,确定点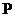 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
、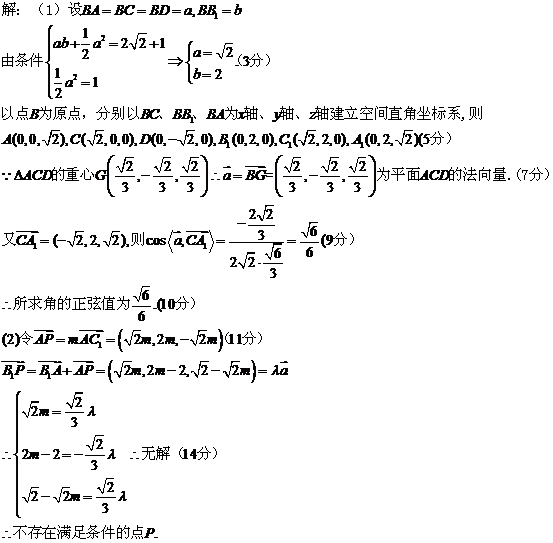
1浙江省金华十校2008-2009学年高三第一学期期末考试数 学 试 题(理科))
(本题满分14分)
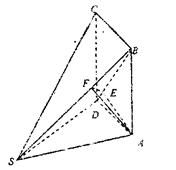
如图,多面体ABCDS中,面ABCD为矩形,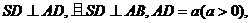
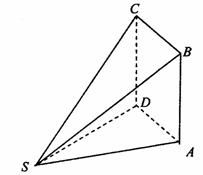
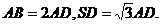
(I)求多面体ABCDS的体积;
(II)求AD与SB所成角的余弦值。
(III)求二面角A-SB-D的余弦值。
1.解:(I)多面体ABCDS的体积即四棱锥S-ABCD的体积。
 所以
所以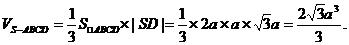 …………4分
…………4分
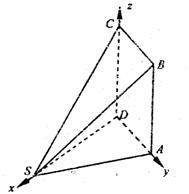
(II)由题可知DA、DA、DC两两互相垂直,
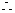 如图建立空间直角坐标系
如图建立空间直角坐标系
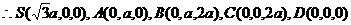
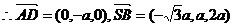
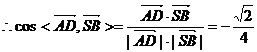
 AD与SB所成的角的余弦为
AD与SB所成的角的余弦为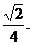 …………9分
…………9分
(III)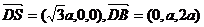 设面SBD的一个法向量为
设面SBD的一个法向量为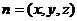
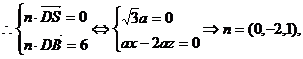
又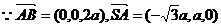
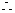 设面SAB的一个法向量为
设面SAB的一个法向量为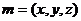
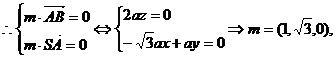 …………11分
…………11分
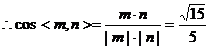 ,
,
所以所求的二面角的余弦为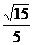 …………14分
…………14分
解法二:(I)同解法一
(II)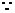 矩形ABCD,
矩形ABCD,
|
 AD//BC,即BC=a,
AD//BC,即BC=a,
 要求AD与SB所成的角,即求BC与SB所成的角。…………6分
要求AD与SB所成的角,即求BC与SB所成的角。…………6分
 在
在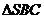 中,由(1)知
中,由(1)知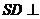 面ABCD。
面ABCD。
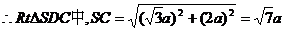
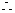 CD是CS在面ABCD内的射影,且
CD是CS在面ABCD内的射影,且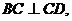
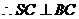
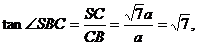
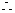 BC与SB所成的角的余弦为
BC与SB所成的角的余弦为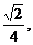
从而SB与AD的成的角的余弦为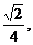 …………9分
…………9分
(III)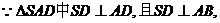
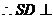 面ABCD。
面ABCD。
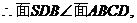 BD为面SDB与面ABCD的交线。
BD为面SDB与面ABCD的交线。
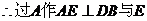
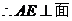 SDB
SDB
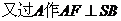 于F,连接EF
于F,连接EF
从而得: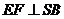
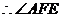 为二面角A-SB-D的平面角…………11分
为二面角A-SB-D的平面角…………11分
在矩形ABCD中,对角线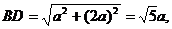
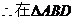 中,
中,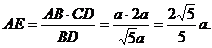
由(2)知在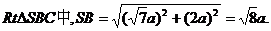
而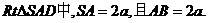
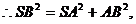
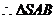 为等腰直角三角形且
为等腰直角三角形且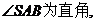
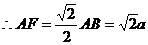
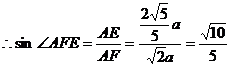 ,
,
所以所求的二面角的余弦为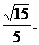 …………14分
…………14分
2(温州中学高三2008学年第一学期期末考试数 学 试 卷文)
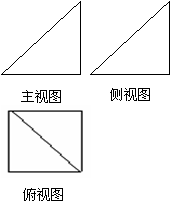
. (本小题满分14分)一个简单多面体的直观图和三视图如图所示,它的主视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形,E是PD的中点.
 (1)求证:
(1)求证: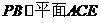 ;
;
(2)求证: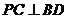 ;
;
(3)求三棱锥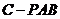 的体积.
的体积.
2.(宁波市2008学年度第一学期高三期末数(文))在平面几何中,有射影定理:“在 中,
中,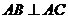 , 点
, 点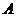 在
在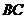 边上的射影为
边上的射影为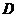 ,有
,有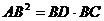 .”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥
.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥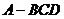 中,
中,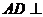 平面
平面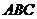 ,点
,点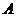 在底面
在底面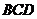 上的射影为
上的射影为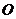 ,则有 .”
,则有 .”
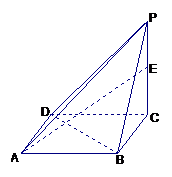
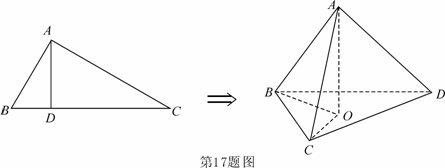
(第2题图)
答案: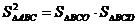
1.(浙江省09年高考省教研室第一次抽样测试数学试题(理))若某多面体的三视图(单位: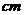 )如图所示,则此多面体的体积是
)如图所示,则此多面体的体积是
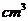 .
.
答案:9
解析:对于这个多面体底面积是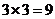 ,而高是3,因此其体积为
,而高是3,因此其体积为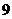 .
.
7.π
7. 如图,一个空间几何体的主视图、侧视图是周长为4一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为 ▲ .
如图,一个空间几何体的主视图、侧视图是周长为4一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的表面积为 ▲ .
6.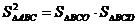
(浙江省嘉兴市高中学科基础测试(理科) 数学试题卷2009.1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com