
2.下列运算正确的是
A. B.
B. C.
C. D.
D.
1.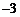 的绝对值是
的绝对值是
A.3 B.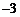 C.
C. D.
D.
25.(2010.十堰)(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
[答案]解:(1)分两种情况讨论:
①当m=0 时,方程为x-2=0,∴x=2 方程有实数根
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,∴方程恒有实数根
综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根.
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标.
则有x1+x2=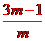 ,x1·x2=
,x1·x2=
由| x1-x2|=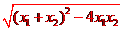 =
= =
=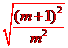 =
=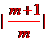 ,
,
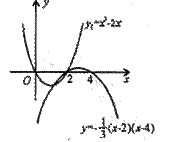 由| x1-x2|=2得
由| x1-x2|=2得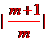 =2,∴
=2,∴ =2或
=2或 =-2
=-2
∴m=1或m=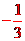
∴所求抛物线的解析式为:y1=x2-2x或y2=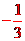 x2+2x-
x2+2x-
即y1= x(x-2)或y2=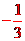 (x-2)(x-4)其图象如右图所示.
(x-2)(x-4)其图象如右图所示.
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围.
 ,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
同理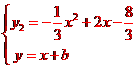 ,可得△=9-4(8+3b)=0,得b=-.
,可得△=9-4(8+3b)=0,得b=-.
观察函数图象可知当b<-或b>-时,直线y=x+b与(2)中的图象只有两个交点.
由
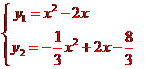
当y1=y2时,有x=2或x=1
当x=1时,y=-1
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上所述可知:当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点.
24.(2010.十堰)(本小题满分9分)如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;
(2)证明:AB·BC=2O2B·BO1;
(3)如果AB·BC=12,O2C=4,求AO1的长.
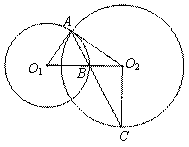

解:(1)∵AO1是⊙O2的切线,∴O1A⊥AO2 ∴∠O2AB+∠BAO1=90°
又O2A=O2C,O1A=O1B,∴∠O2CB=∠O2AB,∠O2BC=∠ABO1=∠BAO1
∴∠O2CB+∠O2BC=∠O2AB+∠BAO1=90°,∴O2C⊥O2B,即O2C⊥O1O2
 (2)延长O2O1交⊙O1于点D,连结AD.
(2)延长O2O1交⊙O1于点D,连结AD.
∵BD是⊙O1直径,∴∠BAD=90°
又由(1)可知∠BO2C=90°
∴∠BAD=∠BO2C,又∠ABD=∠O2BC
∴△O2BC∽△ABD
∴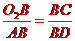
∴AB·BC=O2B·BD 又BD=2BO1
∴AB·BC=2O2B·BO1
(3)由(2)证可知∠D=∠C=∠O2AB,即∠D=∠O2AB,又∠AO2B=∠DO2A
∴△AO2B∽△DO2A
∴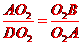
∴AO22=O2B·O2D
∵O2C=O2A
∴O2C2=O2B·O2D ①
又由(2)AB·BC=O2B·BD ②
由①-②得,O2C2-AB·BC= O2B2 即42-12=O1B2
∴O2B=2,又O2B·BD=AB·BC=12
∴BD=6,∴2AO1=BD=6 ∴AO1=3
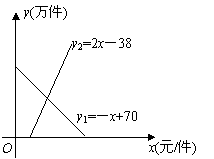
23.(2010.十堰)(本小题满分8分)如图所示,某地区对某种药品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x + 70,y2=2x-38,需求量为0时,即停止供应.当y1=y2时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该药品的稳定价格与稳定需求量.
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.

解:(1)由题可得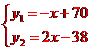 ,
,
当y1=y2时,即-x+70=2x-38
∴3x=108,∴x=36
当x=36时,y1=y2=34,所以该药品的稳定价格为36元/件,稳定需求量为34万件.
(2)令y1=0,得x=70,由图象可知,当药品每件价格在大于36元小于70元时,该药品的需求量低于供应量.
(3)设政府对该药品每件价格补贴a元,则有
 ,解得
,解得
所以政府部门对该药品每件应补贴9元.
22.(2010.十堰)(本小题满分8分)如图所示,直线AB与反比例函数图像相交于A,B两点,已知A(1,4).
(1)求反比例函数的解析式;


(2)连结OA,OB,当△AOB的面积为时,求直线AB的解析式.
解:(1)设反比例函数解析式为y= ,
∵点A(1,4)在反比例函数的图象上
∴4= ,∴k=4,∴反比例函数的解析式为y=
,∴k=4,∴反比例函数的解析式为y= .
.
 (2)设直线AB的解析式为y=ax+b(a>0,b>0),则当x=1时,a+b=4即b=4-a.
(2)设直线AB的解析式为y=ax+b(a>0,b>0),则当x=1时,a+b=4即b=4-a.
联立 ,得ax2 +bx-4=0,即ax2 +(4-a)x-4=0,
,得ax2 +bx-4=0,即ax2 +(4-a)x-4=0,
方法1:(x-1)(ax+4)= 0,解得x1=1或x=-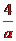 ,
,
设直线AB交y轴于点C,则C(0,b),即C(0,4-a)
由S△AOB=S△AOC+S△BOC= ,整理得
,整理得
a2+15a-16=0,∴a=1或a=-16(舍去) ∴b=4-1=3
∴ 直线AB的解析式为y=x+3
方法2:由S△AOB= |OC|·|x2-x1|=
而|x2-x1|=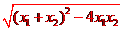 =
=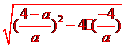 =
= =
=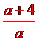 (a>0),
(a>0),
|OC|=b=4-a,可得 ,解得a=1或a=-16(舍去).
,解得a=1或a=-16(舍去).
21.(2010.十堰)(本小题满分8分)暑假快到了,老家在十堰的大学生张明与王艳打算留在上海,为世博会做义工.学校争取到6个义工名额,分别安排在中国馆园区3个名额,世博轴园区2个名额,演义中心园区1个名额. 学校把分别标号为1、2、3、4、5、6的六个质地大小均相同的小球,放在不透明的袋子里,并规定标号1、2、3的到中国馆,标号4、5到世博轴,标号6的到演艺中心,让张明、王艳各摸1个.
(1)求张明到中国馆做义工的概率;
(2)求张明、王艳各自在世博轴、演艺中心做义工的概率(两人不同在一个园区内).
解:(1)如表所示,张明、王艳各摸一球可能出现的结果有6×5=30个,它们出现的可能性相等,张明到中国馆的结果有15个,∴P(张明到中国馆做义务)= .
.
|
张明 王艳 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
(2,1) |
(3,1) |
(4,1) |
(5,1) |
(6,1) |
|
2 |
(1,2) |
|
(3,2) |
(4,2) |
(5,2) |
(6,2) |
|
3 |
(1,3) |
(2,3) |
|
(4,3) |
(5,3) |
(6,3) |
|
4 |
(1,4) |
(2,4) |
(3,4) |
|
(5,4) |
(6,4) |
|
5 |
(1,5) |
(2,5) |
(3,5) |
(4,5) |
|
(6,5) |
|
6 |
(1,6) |
(2,6) |
(3,6) |
(4,6) |
(5,6) |
|
(2)张明、王艳各自在世博轴、演艺中心的结果共4个,其概率P= .
.
20.(2010.十堰)(本小题满分8分)某乡镇中学数学活动小组,为测量数学楼后面的山高AB,用了如下的方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的仰角为45°.已知教学楼高CD=12米,求山高AB.(参考数据=1.73,=1.41,精确到0.1米,化简后再代入参考数据运算)




解:过D作DE⊥AB于E,而AB⊥BC,DC⊥BC,故四边形DEBC为矩形,
则CD=BE,∠ADE=45°,∠ACB=60°.
设AB=h 米,在Rt△ABC中,BC=h·cot60°=h·tan30°= h
h
在Rt△AED中,AE=DE·tan45°=BC·tan45°= h
h
又AB-AE=BE=CD=12
∴h- h=12
h=12
∴h=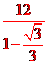 =
= =18+6×1.73=18+10.38≈28.4(米)
=18+6×1.73=18+10.38≈28.4(米)
答:山高AB是28.4米.
19.(2010.十堰)(本小题满分7分)如图,△ABC中,AB=AC,BD⊥AC,
CE⊥AB.
求证:BD=CE.


证明:∵BD⊥AC,CE⊥AB
∴∠ADB=∠AEC=90°
在△ABD和△AEC中,∠ADB=∠AEC=90°,∠A=∠A,AB=AC
∴△ABD≌△AEC
∴BD=CE.
18.(2010.十堰)(本小题满分7分)
先化间,再求值: ,其中
,其中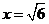 .
.
解:原式= (x+1)(x-1)+(x-2)
(x+1)(x-1)+(x-2)
=x(x-1)+(x-2)
=x2-2
当x=时,原式=()2-2=4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com