23．(本题满分10分)

在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x(h)后，与B港的距离分别为、(km)，、与x的函数关系如图所示．

(1)填空：A、C两港口间的距离为　　 km，　　 ；

(2)求图中点P的坐标，并解释该点坐标所表示的实际意义；

(3)若两船的距离不超过10 km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．

22．(本题满分10分)

问题背景

(1)如图1，△ABC中，DE∥BC分别交AB，AC于D，E两点，

过点E作EF∥AB交BC于点F．请按图示数据填空：

四边形DBFE的面积　　　 ，

△EFC的面积　　　 ，

△ADE的面积　　　 ．

探究发现

(2)在(1)中，若，，DE与BC间的距离为．请证明．

拓展迁移

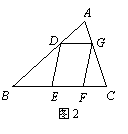
(3)如图2，□DEFG的四个顶点在△ABC的三边上，若

△ADG、△DBE、△GFC的面积分别为2、5、3，试利用(2)

中的结论求△ABC的面积．

21．(本题满分9分)

某联欢会上有一个有奖游戏，规则如下：有5张纸牌，背面都是喜羊羊头像，正面有2张是笑脸，其余3张是哭脸．现将5张纸牌洗匀后背面朝上摆放到桌上，若翻到的纸牌中有笑脸就有奖，没有笑脸就没有奖．

(1)小芳获得一次翻牌机会，她从中随机翻开一张纸牌．小芳得奖的概率是　　　　 ．

(2)小明获得两次翻牌机会，他同时翻开两张纸牌．小明认为这样得奖的概率是小芳的两倍，你赞同他的观点吗？请用树形图或列表法进行分析说明．

20．(本题满分9分)

如图，在⊙O中，直径AB垂直于弦CD，垂足为E，连接AC，

将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．

(1)直线FC与⊙O有何位置关系？并说明理由；

(2)若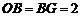，求CD的长．

19．(本题满分8分)

已知二次函数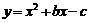的图象与轴两交点的坐标分别为(，0)，(，0)()．

(1)证明；

(2)若该函数图象的对称轴为直线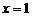，试求二次函数的最小值．

18．(本题满分8分)

随着人们节能意识的增强，节能产品的销售量逐年增加．某商场高效节能灯的年销售量2008年为5万只，预计2010年将达到7.2万只．求该商场2008年到2010年高效节能灯年销售量的平均增长率．

17．(本题满分6分)

先化简，再求值：，其中．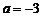

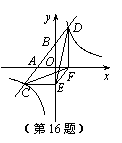
16．如图，一次函数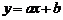的图象与轴，轴交于A，B两点，

与反比例函数的图象相交于C，D两点，分别过C，D两

点作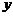轴，轴的垂线，垂足为E，F，连接CF，DE．

有下列四个结论：

①△CEF与△DEF的面积相等；　　　 ②△AOB∽△FOE；

③△DCE≌△CDF；　　　　　 　　　 ④．

其中正确的结论是　　　　　　　　 ．(把你认为正确结论的序号都填上)

14．如图，已知直线∥∥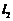∥，相邻两条平行直线间的

距离都是1，如果正方形ABCD的四个顶点分别在四条直

线上，则　　　 ．

第一年 第二年 第三年 … 应还款(万元) 3 … 剩余房款(万元) 9 8.5 8 …

若第年小慧家仍需还款，则第年应还款 　　　　万元(＞1)．

13．如图，直线：与直线：相交于点

P(，2)，则关于的不等式≥的解集为　　 ．