
5.(四川卷文16)设S为复数集C的非空子集.若对任意 ,都有
,都有 ,则
,则
称S为封闭集。下列命题:
①集合S={a+b |
| 为整数}为封闭集;
为整数}为封闭集;
②若S为封闭集,则一定有 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足 的任意集合
的任意集合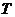 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②
4.(四川卷理16)设S为复数集C的非空子集.若对任意 ,都有
,都有 ,则称S为封闭集。下列命题:
,则称S为封闭集。下列命题:
①集合S={a+bi| 为整数,
为整数,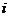 为虚数单位}为封闭集;
为虚数单位}为封闭集;
②若S为封闭集,则一定有 ;
;
③封闭集一定是无限集;
④若S为封闭集,则满足 的任意集合
的任意集合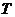 也是封闭集.
也是封闭集.
其中真命题是 (写出所有真命题的序号)
解析:直接验证可知①正确.
当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确
对于集合S={0},显然满足素有条件,但S是有限集,③错误
取S={0},T={0,1},满足 ,但由于0-1=-1ÏT,故T不是封闭集,④错误
,但由于0-1=-1ÏT,故T不是封闭集,④错误
答案:①②
3.(湖南卷文15)若规定E= 的子集
的子集 为E的第k个子集,其中k=
为E的第k个子集,其中k= ,则(1)
,则(1) 是E的第____个子集;(2)E的第211个子集是_______
是E的第____个子集;(2)E的第211个子集是_______
[答案](1) 是E的第___5_个子集;
是E的第___5_个子集;
(2)E的第211个子集是___ ____
____
2.(湖南卷理15)若数列 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得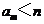 成立,记这样的
成立,记这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 .例如,若数列
.例如,若数列 是
是 ,则数列
,则数列 是
是 .已知对任意的
.已知对任意的 ,
, ,则
,则 ,
, .
.
[答案]2,
[解析]因为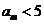 ,而
,而 ,所以m=1,2,所以
,所以m=1,2,所以 2.
2.

所以 =1,
=1,  =4,
=4,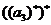 =9,
=9, =16,
=16,
猜想
[命题意图]本题以数列为背景,通过新定义考察学生的自学能力、创新能力、探究能力,属难题。
1.(福建卷文15)对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包涵Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如下(阴影区域及其边界): 其中为凸集的是 (写出所有凸集相应图形的序号).
[答案]②③
[解析]根据题意,在①④中任取两点,连接起来,如下图,不符合题意。




6. (2010江苏卷)14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是____▲____。
,则S的最小值是____▲____。
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小 正三角形的边长为
正三角形的边长为 ,
, 则:
则:
(方法一)利用导数求函数最小值。
 ,
,

 ,
,
当 时,
时, 递减;当
递减;当 时,
时, 递增;
递增;
故当 时,S的最小值是
时,S的最小值是 。
。
(方法二)利用函数的方法求最小值。
令 ,则:
,则:
故当 时,S的最小值是
时,S的最小值是 。
。
5. (2010江苏卷)11、已知函数 ,则满足不等式
,则满足不等式 的x的
的x的 范围是__▲___。
范围是__▲___。
[解析] 考查分段函数的单调性。
4. (2010江苏卷)5、设函数f(x)=x(ex+ ae-x)(x
ae-x)(x R)是偶函数,则实数
R)是偶函数,则实数 a=_______▲_________
a=_______▲_________
[解析]考查函数的奇偶性的知识。g(x)=ex+ae-x为奇函数,由g(0)=0,得a=-1。
3. (2010福建理数)15.已知定义域为 的函数
的函数 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;当
成立;当 时,
时, 。给出如下结论:
。给出如下结论:
①对任意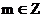 ,有
,有 ;②函数
;②函数 的值域为
的值域为 ;③存在
;③存在 ,使
,使 得
得 ;④“函数
;④“函数 在区间
在区间 上单调递减”的充要条件是
“存在
上单调递减”的充要条件是
“存在 ,使得
,使得
 ”。
”。
其 中所有正确结论的序号是
。
中所有正确结论的序号是
。
[答案]①②④
[解析]对①,因为 ,所以
,所以 ,故①正确;经分析,容易得出②④也正确。
,故①正确;经分析,容易得出②④也正确。
[命题意图]本题考查函数的性质与充要条件,熟练基础知识是解答好本题的关键。
14.(2010湖南理数)过抛物线 的焦点作斜率为1的
的焦点作斜率为1的 直线与该抛物线交于
直线与该抛物线交于 两点,
两点, 在
在 轴上的正射影分别为
轴上的正射影分别为 .若梯形
.若梯形
 的面积为
的面积为 ,则
,则 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com