
2.1≤x2-2x<3 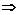

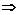
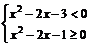
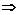
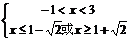
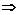 -1<x≤1-
-1<x≤1-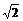 或 1+
或 1+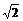 ≤x<3
≤x<3
一元二次不等式 ax2+bx+c>0与 ax2+bx+c<0 的解法
(分 △>0, △=0, △<0 三种情况)
1.2x4-x2-1≥0 2.1≤x2-2x<3 (《课课练》 P15 第8题中)
解:1.2x4-x2-1≥0 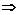 (2x2+1)(x2-1)≥0
(2x2+1)(x2-1)≥0 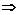 x2≥1
x2≥1
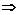 x≤-1 或 x≥1
x≤-1 或 x≥1
《课课练》第8课余下部分
练习:(板演)
有时间多余,则处理《课课练》P14 “例题推荐”
先回忆一下初中学过的一元一次不等式的解法:如 2x-7>0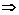 x>
x>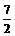
|
 这里利用不等式的性质解题
这里利用不等式的性质解题
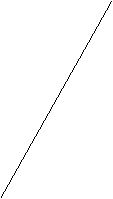 从另一个角度考虑:令 y=2x-7 作一次函数图象:
从另一个角度考虑:令 y=2x-7 作一次函数图象:
|
|
 引导观察,并列表,见 P17 略
引导观察,并列表,见 P17 略
当 x=3.5 时, y=0 即 2x-7=0
当 x<3.5 时, y<0 即 2x-7<0
当 x>3.5 时, y>0 即 2x-7>0
结论:略 见P17
注意强调:1°直线与 x轴的交点x0是方程 ax+b=0的解
2°当 a>0 时, ax+b>0的解集为 {x | x > x0 }
当 a<0 时, ax+b<0可化为 -ax-b<0来解
|
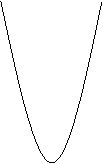
 同样用图象来解,实例:y=x2-x-6 作图、列表、观察
同样用图象来解,实例:y=x2-x-6 作图、列表、观察
|
 当 x=-2 或 x=3 时, y=0 即 x2-x-6=0
当 x=-2 或 x=3 时, y=0 即 x2-x-6=0
当 x<-2 或 x>3 时, y>0 即 x2-x-6>0
当 -2<x<3 时, y<0 即 x2-x-6<0
∴方程 x2-x-6=0 的解集:{ x | x = -2或 x = 3 }
不等式 x2-x-6 > 0 的解集:{ x | x < -2或 x > 3 }
不等式 x2-x-6 < 0 的解集:{ x | -2 < x < 3 }
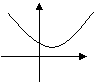
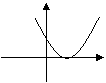 这是 △>0 的情况:
这是 △>0 的情况:
若 △=0 , △<0 分别作图观察讨论
得出结论:见 P18--19
说明:上述结论是一元二次不等式 ax+bx+c>0(<0) 当 a>0时的情况
若 a<0, 一般可先把二次项系数化成正数再求解
3、预习下一课。
教学反思
2、完成课后练习题。
1、熟读课文,背诵有关语段“那柔曼如提琴者……飞瀑落下深潭”,并且仿造它自己另造一个句子。
本文是一篇写景散文,按照游者的行踪把所见所闻表现出来,但它并不是简单地写景,而在对景物的描写中透露出对人生的见解。
这一节课,我们领略了鼎湖山泉水的独特魅力。泉声听在耳里,泉水流进心田,这样的泉水怎不叫人难忘呢?愿这滋润万物的泉水汩汩地流进我们的心田,愿这音乐般美妙的泉声永远铭记在我们的心田。
5、由于引来了大批旅游者,鼎湖山发生什么变化?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com