10、方程x²-ax+b=0的两实根为m,n,方程x²-bx+c=0的两实根为p,q,其中m、n、p、q互不相等，集合A={m,n,p,q},作集合S={x|x=a+b,aÎA,bÎA且a¹b}，P={x|x=ab,aÎA,bÎA且a¹b},若已知S={1,2,5,6,9,10},P={-7,-3,-2,6,

14,21}求a,b,c的值。

解：由根与系数的关系知：m+n=a　 mn=b　 p+q=b　 pq=c

又: mnÎP 　p+qÎS 即 bÎP且 bÎS

∴ bÎP∩S 又由已知得 S∩P={1,2,5,6,9,10}∩{-7,-3,-2,6,14,21}={6}

∴b=6

又：S的元素是m+n,m+p,m+q,n+p,n+q,p+q其和为

3(m+n+p+q)=1+2+5+6+9+10=33　 ∴m+n+p+q=11　 即 a+b=11

由 b=6得　 a=5

又：P的元素是mn,mp,mq,np,nq,pq其和为

mn+mp+mq+np+nq+pq=mn+(m+n)(p+q)+pq=-7-3-2+6+14+21=29

且 mn=b　 m+n=a　 p+q=b　 pq=c

即 b+ab+c=29　 再把b=6 , a=5 代入即得　 c=-7

∴a=5, b=6, c=-7

9、设集合A={xÎR|x²+6x=0},B={ xÎR|x²+3(a+1)x+a²-1=0}且A∪B=A求实数a的取值。

解：A={xÎR|x²+6x=0}={0,-6}　 由A∪B=A 知 BÍA

当B=A时　 B={0,-6}　 　Þ a=1　 此时 B={xÎR|x²+6x=0}=A

当B　 A时　

　 　1^。若 B¹F 则 B={0}或 B={-6}

由 D=[3(a+1)]²-4(a²-1)=0 即5a²+18a+13=0 解得a=-1或 a=-

当a=-1时 x²=0　 ∴B={0}　 满足B　 A

当a=-时 方程为 　x₁=x₂=

∴B={}　 则 BÍA(故不合，舍去)

　 　2^。若B=F 即 D<0 由 D=5a²+18a+13<0　 解得-<a<-1

此时 B=F 也满足B　 A

综上: -<a≤-1或 a=1

8、设A={x|-3≤x≤a}, B={y|y=3x+10,xÎA}, C={z|z=5-x,xÎA}且B∩C=C求实数a的取值。

解：由A={x|-3≤x≤a} 必有a≥-3 由-3≤x≤a知

3×(-3)+10≤3x+10≤3a+10

故　 1≤3x+10≤3a+10 于是 B={y|y=3x+10,xÎA}={y|1≤y≤3a+10}

又 -3≤x≤a　 ∴-a≤-x≤3　　　 5-a≤5-x≤8

∴C={z|z=5-x,xÎA}={z|5-a≤z≤8}

由B∩C=C知 CÍB 　由数轴分析:且 a≥-3

Þ -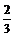≤a≤4 且都适合a≥-3

　综上所得:a的取值范围{a|-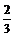≤a≤4 }

7、设 A∩B={3},　 (CuA)∩B={4,6,8},　 A∩(CuB)={1,5},　 (CuA)∪(CuB)

={xÎN*|x<10且x¹3} , 求Cu(A∪B), A, B。

解一： (CuA)∪(CuB) =Cu(A∩B)={xÎN*|x<10且x¹3} 又：A∩B={3}

　　　 U=(A∩B)∪Cu(A∩B)={ xÎN*|x<10}={1,2,3,4,5,6,7,8,9}

　　　 A∪B中的元素可分为三类:一类属于A不属于B;一类属于B不属于A;一类既属A又属于B

由(C_uA)∩B={4,6,8}　 即4,6,8属于B不属于A

由(C_uB)∩A={1,5}　　 即　 1,5 属于A不属于B

由A∩B ={3}　　　　 即　 3 既属于A又属于B

∴A∪B ={1，3，4，5，6，8}

∴C_u(A∪B)={2，7，9}

A中的元素可分为两类:一类是属于A不属于B,另一类既属于A又属于B

　　　 ∴A={1,3,5}

同理 　B={3,4,6,8}

6、设A={x|x=12m+28n,m、nÎZ}, B={x|x=4k,kÎZ} 求证:1^。 8ÎA　 2^。 A=B

证：1^。若12m+28n=8 则m=　 当n=3l或n=3l+1(lÎZ)时

m均不为整数　 当n=3l+2(lÎZ)时 m=-7l-4也为整数

不妨设 l=-1则 m=3,n=-1　　　 ∵8=12×3+28×(-1) 且 3ÎZ　 -1ÎZ

∴8ÎA

2^。任取x₁ÎA　 即x₁=12m+28n　 (m,nÎZ)

由12m+28n=4=4(3m+7n) 且3m+7nÎZ 而B={x|x=4k,kÎZ}

∴12m+28nÎB 即x₁ÎB 于是AÍB

任取x₂ÎB　 即x₂=4k, kÎZ

由4k=12×(-2)+28k 且 -2kÎZ 而A={x|x=12m+28n,m,mÎZ}

∴4kÎA 即x₂ÎA 于是 BÍA

综上：A=B

5、设U={xÎN|x<10}, A={1,5,7,8}, B={3,4,5,6,9}, C={xÎN|0≤2x-3<7}　 求：

A∩B,A∪B,(C_uA)∩(C_uB), (C_uA)∪(C_uB),A∩C, [C_u(C∪B)]∩(C_uA)。

解：U={xÎN|x<10}={0,1,2,3,4,5,6,7,8,9},　 　C={xÎN|≤x<5}={2,3,4}

A∩B={5}　 A∪B={1,3,4,5,6,7,8,9}

　　 ∵CuA={0,2,3,4,6,9}　　 CuB={0,1,2,7,8}

　　 ∴(CuA)∩(CuB)={0,2}　 (CuA)∪(CuB)={0,1,2,3,4,6,7,8,9}

　　 A∩C=F　 又 ∵C∪B={2,3,4,5,6,9}　 ∴Cu(C∪B)={0,1,7,8}

　　 ∴[Cu(C∪B)]∩(CuA)={0}

4、求满足{1}　 AÍ{1,2,3,4,5}的所有集合A。

解：由题设：二元集A有 {1，2}、{1，3}、{1，4}、{1，5}

三元集A有 {1，2，3}、{1，2，4}、{1，2，5}、{1，3，4}、{1，3，5}、{1，4，5}

四元集A有 {1，2，3，4}、{1，2，3，5}、{1，2，4，5}、{1，3，4，5}

五元集A有 {1，2，3，4，5}

3、已知集合A={x,x²,y²-1}, B={0,|x|,y} 且 A=B求x,y。

解：由A=B且0ÎB知 0ÎA

若x²=0则x=0且|x|=0 不合元素互异性，应舍去

若x=0 则x²=0且|x|=0 也不合

∴必有y²-1=0 得y=1或y=-1

若y=1 则必然有1ÎA,　 若x=1则x²=1　 |x|=1同样不合，应舍去

若y=-1则-1ÎA 只能 x=-1这时 x²=1,|x|=1　 A={-1,1,0} B={0,1,-1}

即 A=B

综上所述： x=-1, y=-1

　　 1、用适当的符号(Î，Ï， ， ，=，Í)填空：

0 Ï F；　 0 Î N；　 F　　 {0}； 2 Î 　{x|x-2=0}；

{x|x²-5x+6=0} = {2,3}；　　 (0,1)　 Î {(x,y)|y=x+1}；

{x|x=4k,kÎZ}　 {y|y=2n,nÎZ}；　 {x|x=3k,kÎZ} Í　 {x|x=2k,kÎZ}；

{x|x=a²-4a,aÎR}　 {y|y=b²+2b,bÎR}

2、用适当的方法表示下列集合，然后说出其是有限集还是无限集。

　 ① 由所有非负奇数组成的集合； {x=|x=2n+1,nÎN} 无限集

　 ② 由所有小于20的奇质数组成的集合； {3,5,7,11,13,17,19} 有限集

　 ③ 平面直角坐标系内第二象限的点组成的集合； {(x,y)|x<0,y>0} 无限集

　 ④ 方程x²-x+1=0的实根组成的集合； F　 有限集

　 ⑤ 所有周长等于10cm的三角形组成的集合；

{x|x为周长等于10cm的三角形}　 无限集

3．集合与集合间的运算关系：全集与补集、交集、并集