提问(板演)：U={x|0≤x<6,xÎZ}　　 A={1,3,5}　 B={1,4}

　　　　　 求：CuA= {0,2,4}．　　 CuB= {0,2,3,5}．

　　　　　 《教学与测试》 P18 5、6、7、8 及“思考题”

　　　　 　2^。 于二次函数在闭区间上的最值问题应注意顶点的位置。

3．次之，还必须结合抛物线的开口方向，“顶点”在区间中点的左侧还是右侧综合判断。

处理《课课练》 P20“例题推荐”中例一至例三　 略

2．关键是“顶点”是否在给定的区间内；

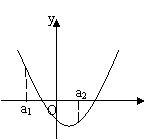
1．必须是“闭区间” a₁≤x≤a₂

例题：《教学与测试》P17-18例一至例三　 略

　　 《课课练》 P19 “例题推荐”　 3

　　　 关于x的不等式对一切实数x恒成立， 求实数k的取值范围。

　　　 解：∵ x²-x+3>0恒成立　 ∴ 原不等式可转化为不等式组：

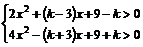　 　由题意上述两不等式解集为实数

∴ 　　

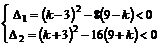
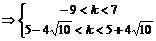
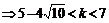
即为所求。

《课课练》P13 第10题：

　　　　 设A=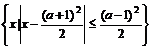　 B={x|2≤x≤3a+1}是否存在实数a的值，分别使得：(1) A∩B=A　　 (2)A∪B=A

　　　　 解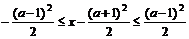：∵　　 ∴ 2a≤x≤a²+1

　　　　　　 ∴ A={x|2a≤x≤a²+1}

　　　　　　 (1) 若A∩B=A　 则AÍB　　 ∴ 2≤2a≤a²+1≤3a+1　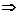 　1≤a≤3

　　　　　　 (2) 若A∪B=A　 则BÍA　　

　　　　　　　　　　　　 ∴当B=Ø时 2>3a+1　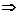 　a<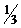

　　　　　　　　　　　　　 当B¹Ø时 2a≤2≤3a+1≤a²+1　 无解

　　　　　　 ∴ a<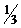

(2)讨论，打开绝对值符号

2．一元二次不等式的解法：利用法则(图形法)