
|
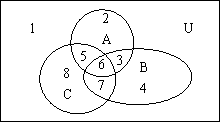
区域号 |
相应的集合 |
|
1 |
CUA∩CUB |
|
2 |
A∩CUB |
|
3 |
A∩B |
|
4 |
CUA∩B |
|
集合 |
相应的区域号 |
|
A |
2,3 |
|
B |
3,4 |
|
U |
1,2,3,4 |
|
A∩B |
3 |
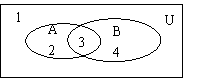
图(1)
图(2)
2.如图(2) U是全集,A,B,C是U的三个子集,图中有8个用数字标
出的区域,试填下表: (见右半版)
《课课练》 P8-9 课时5中选部分
规定:集合A 的元素个数记作: card (A)
 作图
观察、分析得:
作图
观察、分析得:
card (A∪B) ¹ card (A) + card (B)
card (A∪B) = card (A) +card (B) -card (A∩B)
例7 ( P12 ) 略
练习 P13
A∪A = A, A∪φ= A , A∪B = B∪A.
(注意与实数性质类比)
例6 ( P12 ) 略
进而讨论 (x,y) 可以看作直线上的点的坐标
A∩B 是两直线交点或二元一次方程组的解
同样设 A = {x | x2-x-6 = 0} B = {x | x2+x-12 = 0}
则 (x2-x-6)(x2+x-12) = 0 的解相当于 A∪B
即: A = {3,-2} B = {-4,3} 则 A∪B = {-4,-2,3}
补充:设集合A
= {x | -4≤x≤2},
B = {x | -1≤x≤3},
C = {x |x≤0或x≥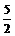 },
},
求A∩B∩C, A∪B∪C。
《课课练》 P 6--7 “基础训练题”及“ 例题推荐”
解:
∵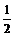 ÎA且
ÎA且 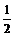 ÎB
∴
ÎB
∴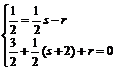
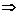

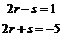
解之得 s= -2 r= -
∴A={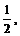 -
- } B={
} B={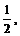 -
-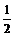 }
}
∴A∪B={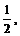 -
- ,-
,-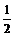 }
}
3、例题:课本P11例一至例五
练习P12
补充: 例一、设A={2,-1,x2-x+1}, B={2y,-4,x+4}, C={-1,7} 且A∩B=C求x,y。
解:由A∩B=C知 7ÎA ∴必然 x2-x+1=7 得
x1=-2, x2=3
由x=-2 得 x+4=2ÏC ∴x¹-2
∴x=3 x+4=7ÎC 此时 2y=-1 ∴y=-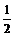
∴x=3
, y=-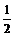
2、定义: 交集: A∩B ={x|xÎA且xÎB} 符号、读法
并集: A∪B ={x|xÎA或xÎB}
见课本P10--11 定义 (略)
1、实例: A={a,b,c,d} B={a,b,e,f}
图
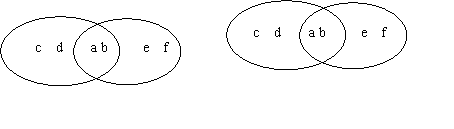
公共部分 A∩B 合并在一起 A∪B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com