4．例一　　 见　 P30　 例一　 略

　 注意：关键是找出原命题的条件(p)，结论(q)

　　　　 然后适当改写成更明显的形式。

3．若p为原命题条件，q为原命题结论

　 则：原命题：若 p 则 q　　　 　逆命题：若 p 则 q

　　　 否命题：若 Øp 则 Øq　　 　逆否命题：若 Øq 则 Øp

2．概括：(1)为原命题　　　　　　 (2)为逆命题　

(3)为否命题　　　　　　 (4)为逆否命题

1．看两个命题：同位角不相等，两直线不平行　　　　　　　 (3)

　　　　　　　　　　 两直线不平行，同位角不相等　　　　　　　 (4)

　　　　 比较命题(1)与(3)：一个命题的条件和结论，分别是另一个命题的条件的否定和结论的否定。…………互否命题

　　　　 比较命题(1)与(4)：一个命题的条件和结论，分别是另一个命题的结论的否定和条件的否定。……互为逆否命题

　　　 定义：如果第一个命题的条件(或题设)是第二个命题的结论，且第一个命题的结论是第二个命题的条件，这两个命题叫互逆命题。其中一个命题叫做原命题，另一个命题叫做原命题的否命题。

　　　 例：“同位角相等，两直线平行”　　　　　　　　　　　　　 (1)

　　　　 条件(题设)：同位角相等。　　 结论：两直线平行

　　　　 它的逆命题：两直线平行，同位角相等。 　　　　　　　　(2)

　　 例　 | x | > 2与 | x | < 2

　 1°从数轴上，绝对值的几何意义出发分析、作图。解之、见 P15　 略

　　 结论：不等式 　| x | > a　 的解集是　　 { x | -a< x < a}

　| x | < a　 的解集是　　 { x | x > a 或 x < -a}

　 2°从另一个角度出发：用讨论法打开绝对值号

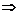
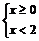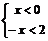　　 | x | < 2　 　　或 　Þ 0 ≤ x < 2或-2 < x < 0

　　　　　　 合并为 { x | -2 < x < 2}

　　 同理 | x | < 2　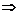 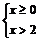　　或 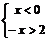　Þ { x | x > 2或 x < -2}

3°例题　 P15　　 例一、例二　　 略

4°《课课练》　 P12　 “例题推荐”

　　 复习绝对值意义：| a | =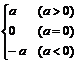

　　　 几何意义：数轴上表示 a 的点到原点的距离

　 实例：课本 P14(略) 得出两种表示方法：

1．不等式组表示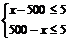：　　　 2．绝对值不等式表示:：| x - 500 | ≤5

　 课题：含绝对值不等式解法

证：假设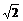是有理数，则不妨设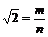(m,n为互质正整数)

　　 从而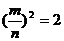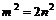：，，可见m是偶数。

设m=2p(p是正整数)，则 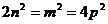，可见n 是偶数。

这样，m.,n就不是互质的正整数(矛盾)。∴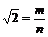不可能

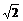∴不是有理数。

证明：反设AB、CD被P平分

∵P不是圆心，连结OP

则由垂径定理：

OP^AB，OP^CD

则过P有两条直线与OP垂直(矛盾)

∴弦AB，CD不被P平分