1．集合的概念　 含集合三要素

　　　　　 《课课练》16课余下部分

又例：命题“若 x = y 则 x² = y²”写出它的逆命题、否命题、逆否命题，并判断它的真假。

解：逆命题：若 x² = y² 则 x = y　　　 (假，如 x = 1, y = -1)

否命题：若 x ¹ y 则 x² ¹ y²　　　 (假，如 x = 1, y = -1)

逆否命题：若 x² ¹ y² 则 x ¹ y　　 (真)

又例：写出命题：“若 x + y = 5则 x = 3且 y = 2”的逆命题否命题逆否命题，并判断它们的真假。

解：逆命题：若 x = 3 且 y = 2 则 x + y = 5　　 (真)

否命题：若 x + y ¹ 5 则 x ¹ 3且y¹2　　　 　(真)

逆否命题：若 x ¹ 3 或y¹2 则 x + y ¹5　　 (假)

3．又例：若四边形 ABCD为平行四边形，则对角线互相平分。

　　　 　　　　它的逆命题、否命题、逆否命题均为真。

2．如果原命题为真，则逆命题、否命题、逆否命题真假如何？

　　　 　例：原命题：“若 a = 0 则 ab = 0”是真命题

　　　　 　　逆命题：“若 ab = 0 则 a = 0”是假命题

否命题：“若 a ¹ 0 则 ab ¹ 0”是假命题

逆否命题：“若 ab ¹ 0 则 a ¹ 0”是真命题

　　 　小结：原命题为真，逆命题不一定为真，

否命题也不一定为真，逆否命题为真。

1．接复习提问：原命题与逆否命题互逆否，否命题与逆命题互逆否，逆命题与逆否命题互逆。

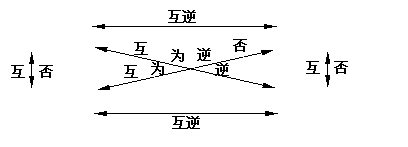　　　 小结：得表：

提问：说出命题“若两个三角形全等，则这两个三角形相似”的逆命题、

否命题、逆否命题。(解答略)

　　 《课课练》P28-29 课时15中选部分

例：写出命题“若 xy= 0 则 x = 0或 y = 0”的逆命题、否命题、逆否命题

　 解：逆命题：若 x = 0或 y = 0　　 则 xy = 0

　　　 否命题：若 xy ¹ 0　　　　　 则 x ¹ 0且 y ¹ 0

　　　 逆否命题：若 x ¹ 0且 y ¹ 0　 则 xy¹0

5．注意：1°为什么称“互为”逆命题(否命题，逆否命题)

2°要重视对命题的剖析：条件、结论