
定义:可以判断真假的语句叫命题。正确的叫真命题,错误的叫假命题。
如:①②是真命题,③是假命题
反例:3是12的约数吗? x>5 都不是命题
不涉及真假(问题) 无法判断真假
上述①②③是简单命题。 这种含有变量的语句叫开语句(条件命题)。
例1、解不等式 
解:原不等式可化为:①  和②
和② 
解①: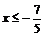 解②:
解②: 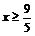
∴原不等式的解集是{x|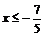 }∪{x|
}∪{x| }={x|
}={x|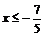 或
或 }
}
例2、解不等式 
解:原不等式可化为:

∴  ∴原不等式的解集是{x|
∴原不等式的解集是{x|  }
}
或解:原不等式化为 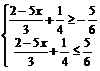 (略)
(略)
例3、解关于x的不等式  (aÎR)
(aÎR)
解:原不等式可化为:
当 a+1>0 即a>-1时 -(a+1)<2x+3<a+1 
当 a+1≤0即 a≤-1时 解集为Ø
∴当a>-1时 原不等式的解集是 {x| };
};
当a≤-1时 解集为Ø
例4、解不等式 
解一:原不等式可化为: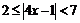
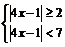


解二: ∵  ∴ Ⅰ:
∴ Ⅰ: Ⅱ:
Ⅱ:
(下略)
解三:原不等式解集等价于下面两个不等式解集的并集:2≤1-4x<7
2≤-(1-4x)<7
(下略)
例5、解不等式 |x+2| + |1-x|<x-4
解:原不等式即为 |x+2| + |x-1|<x-4
Ⅰ: 
 Ø
Ø
Ⅱ: 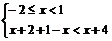
 -1<x<1
-1<x<1
Ⅲ: 
 1≤x<3
1≤x<3
∴ 原不等式的解集为:{x|-1<x<3}
例6、解下列不等式:
① 3-6x-2x2<0
解:整理得 2x2+6x-3<0用求根公式求根得解集{x|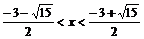 }
}
② (x-1)(3-x)<x(x+1)+1
解:整理得 2x2-3x+4>0 ∵ ∴不等式解集为 R
∴不等式解集为 R
③ 
解:移项,通分,整理得  不等式解集为{x|x≤-4或x>
不等式解集为{x|x≤-4或x> }
}
或解:取并集 

④ 0≤x2-2x-3<5
解:原不等式的解集为下面不等式组的解集


∴原不等式的解集为 {x|-2<x≤-1 或 3≤x<4}
例7、已知U=R且 A={x|x2-5x-6<0} B={x| |x-2|≥1} 求:
1)A∩B 2)A∪B 3)(CuA)∩(CuB)
解:A={x|-1<x<6} B={x|x≤1或x≥3}
A∩B={x|-1<x≤1或3≤x<6} A∪B=R
CuA={x|x≤-1或x≥6} CuB={x|1<x<3}
∴(CuA)∩(CuB)= {x|x≤-1或x≥6}∪{x|1<x<3}=Ø
也可求 Cu(A∪B)= Ø
例8、解关于x的不等式 (1-a)x2+4ax-(4a+1)>0 (aÎR)
解:1 当1-a=0即 a=1时 原不等式化为 4x-5>0 x>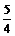
2 当 1-a>0即a<1时 ∵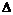 =4(3a+1)
=4(3a+1)
(1)当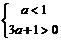 即
即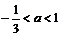 时
时 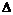 >0
>0
此时原不等式的解集是
(2)当a=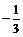 时
时 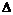 =0 原不等式化为 4x2-4x+1>0 即 (2x-1)2>0
=0 原不等式化为 4x2-4x+1>0 即 (2x-1)2>0
此时原不等式的解集是 {xÎR|x¹ }
}
(3)当a<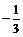 时
时 <0 且 1-a>0 此时原不等式的解集为R
<0 且 1-a>0 此时原不等式的解集为R
3 当1-a<0即a>1时 原不等式可化为 (a-1)x2-4ax+(4a+1)<0
这样a-1>0这时 =4(3a+1)>0 用求根公式求得:
=4(3a+1)>0 用求根公式求得:
此时原不等式的解集为:
综上可得:当a<- 时原不等式解集为R
时原不等式解集为R
当a=- 时原不等式解集为{xÎR|x¹
时原不等式解集为{xÎR|x¹ }
}
当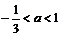 时原不等式解集为
时原不等式解集为
当a=1时原不等式解集为{x| x>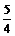 }
}
当a>1时原不等式解集为
例9、已知A={x| |x-a|≤1} B={x|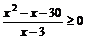 }且A∩B=Ø求a的范围。
}且A∩B=Ø求a的范围。
解:化简A={a-1≤x≤a+1}
由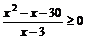

 ≥0 介绍“标根法”
≥0 介绍“标根法”
B={x|-5≤x<3 或 x≥6}
要使A∩B=Ø必须满足 a+1<-5 或  即a<-6或4≤a<5
即a<-6或4≤a<5
∴ 满足条件的a的范围是a<-6或4≤a<5
例10、(1)若不等式 (1-a)x2-4x+6>0的解集是{x|-3<x<1}, 求a的值;
(2)若-3<x<1时 (1-a)x2-4x+6>0成立, 求a的取值范围。
解:(1)由题设可知 1-a<0 

(2)设 y=(1-a)x2-4x+6
1。当1-a>0即a<1时 抛物线开口向上 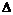 =24a-8
=24a-8
当a< 时
时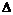 <0 解集为R -3<x<1自然成立
<0 解集为R -3<x<1自然成立
当 <a<1时
<a<1时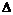 >0 此时对称轴 x=-
>0 此时对称轴 x=- 而x=1时y=3-a>0
而x=1时y=3-a>0
由图象可知: -3<x<1时都有y>0
当a= 时
时  这时对x¹3都有y>0 故-3<x<1时 不等式成立
这时对x¹3都有y>0 故-3<x<1时 不等式成立
∴ a<1时 若-3<x<1不等式(1-a)x2-4x+6>0都成立
2。当a=1时不等式为-4x+6>0对于-3<x<1时 2<-4x+6<18
即-4x+6>0成立
3。当a>1时1-a<0 抛物线开口向下 要使-3<x<1时(1-a)x2-4x+6>0成立
必须 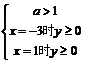
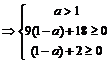

综上:若-3<x<1时(1-a)x2-4x+6>0成立,则a的取值范围是a≤3
1) 方程有两个正根的充要条件;
2) 方程至少有一个正根的充要条件。
解:1) 方程(1-a)x2+(a+2)x-4=0有两个实根的充要条件是: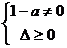
即: Û
Û 
即: a≥10或a≤2且a¹1
设此时方程两根为x1,x2 ∴有两正根的充要条件是:
 Û
Û  Þ 1<a≤2或a≥10 即为所求。
Þ 1<a≤2或a≥10 即为所求。
2) 从1)知1<a≤2或a≥10方程有两个正根
当a=1时, 方程化为 3x-4=0有一个正根x=
方程有一正、一负根的充要条件是:
 Û
Û  Û a<1
Û a<1
综上:方程(1-a)x2+(a+2)x-4=0至少有一正根的充要条件是a≤2或a≥10。
4.ab<0是 |a+b|<|a-b| 的必要而不充分条件。
解:是假命题。|a-b|>|a+b|≥0 Û (a-b)2>(a+b)2 Û a2-2ab+b2> a2+2ab+b2
Û 4ab<0 Û ab<0 ∴(ab<0是 |a+b|<|a-b| 的充要条件)
3.内错角相等是两直线平行的充分条件。
解:是真命题。
2.x2=4x+5是 x 的必要条件。
的必要条件。
解:是假命题。{x| x2=4x+5}={-1,5} {x|
x }={0,5}
}={0,5}
1.(x-2)(x+3)=0是(x-2)2+(y+3)2=0的充要条件。
解:是假命题。反例;若x=2, y¹-3
4.p:0<m<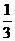 q:方程mx2-2x+3=0有两个同号且不相等的实数根
q:方程mx2-2x+3=0有两个同号且不相等的实数根
则p是q的 充要条件 。
3.p:a与b都是奇数 q:a+b是偶数 则p是q的 充分不必要条件 。
2.p:{x|x>-2或x<3} q:{x|x2-x-6<0} 则p是q的 必要而不充分条件 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com