
17.解:(1)f(x)=2cos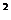 x+
x+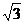 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+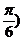
增区间是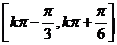 (
( )减区间是
)减区间是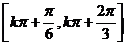 (
( )
)
(2)∵f(A)=2,即1+2sin(2A+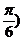 =2,
=2,
∴sin(2A+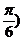 =
=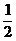
∵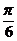 <2A+
<2A+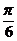 <
<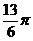 ∴2A+
∴2A+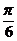 =
= .
.
由cosA=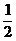 =
=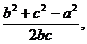 即(b+c)
即(b+c)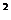 -a
-a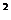 =3bc,
=3bc,
∴bc=2.又b+c=3(b>c), ∴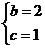
22.(12分)已知曲线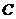 :
: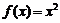 ,
,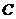 上点
上点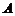 、
、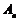 的横坐标分别为
的横坐标分别为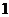 和
和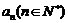 ,且
,且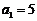 ,
, 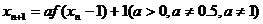 .记区间
.记区间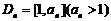 .当
.当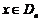 时,曲线
时,曲线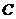 上存在点
上存在点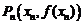 ,使得点
,使得点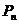 处的切线与直线
处的切线与直线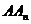 平行.
平行.
(Ⅰ)试证明:数列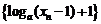 是等比数列;
是等比数列;
(Ⅱ)当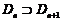 对一切
对一切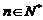 恒成立时,求实数
恒成立时,求实数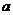 的取值范围;
的取值范围;
文科答案
1-12.  ACBAC ACDAB DB
ACBAC ACDAB DB
13---16. 9, 15, 4, 甲丙
21.( 12分) 已知点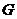 是
是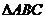 的重心,
的重心,  .在
.在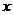 轴上有一点
轴上有一点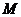 ,满足
,满足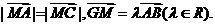
(1)求点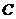 的轨迹方程;
的轨迹方程;
(2)若斜率为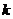 的直线
的直线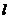 与点
与点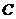 的轨迹交于不同两点
的轨迹交于不同两点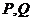 ,且满足
,且满足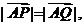 试求
试求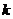 的取值范围.
的取值范围.
20. (12分)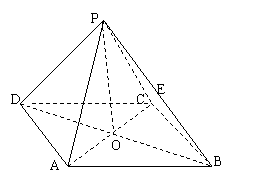 如图所示,正四棱锥
如图所示,正四棱锥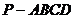 中,侧棱
中,侧棱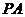 与底面
与底面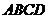 所成角的正切值为
所成角的正切值为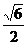 ,
, 为
为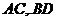 交点.
交点.
(1)求侧面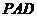 与底面
与底面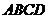 所成二面角的大小;
所成二面角的大小;
(2)若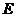 是
是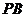 的中点,求异面
的中点,求异面
直线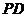 与
与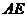 所成角的正切值;
所成角的正切值;
(3)试在侧面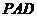 上寻找一点
上寻找一点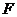 ,
,
使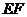 ⊥侧面
⊥侧面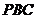 ,确定点
,确定点 的位置,
的位置,
并加以证明 .
19.(12分)设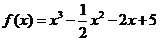
(1)求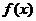 的单调区间,
的单调区间,
(2)当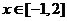 时
时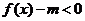 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
18.(12分)一袋中装有大小相同的8个小球,其中5个红球,3个黑球,现从中随机摸出3个球.
(Ⅰ)求至少摸到一个红球的概率;
(Ⅱ)求摸到黑球个数ξ的每个可能取值的概率.
17.(10分)设函数f(x)=2cos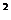 x+
x+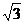 sin2x ,x∈R.
sin2x ,x∈R.
(1) 求f(x)的单调区间;
(2) 在△ABC中,a、b、c分别是角A、B、C的对边,f(A)=2,a=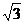 ,b+c=3(b>c),求b、c的长.
,b+c=3(b>c),求b、c的长.

13、 14、 15、 16、
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
16.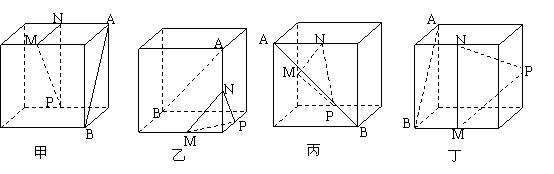 下列四个正方体图形中,
下列四个正方体图形中,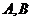 是正方体的两个顶点,
是正方体的两个顶点,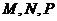 是所在棱的中点,能得出
是所在棱的中点,能得出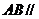 面
面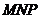 的图形的对应符号是_____甲丙_________________(写出所有符合要求的图形的对应符号).
的图形的对应符号是_____甲丙_________________(写出所有符合要求的图形的对应符号).
高三周考文科数学(三)命题人 周军 2008-11-9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com