
3.D
[解析] ,
,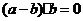 ,所以
,所以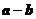 与
与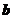 垂直.
垂直.
[规律总结]根据向量是坐标运算,直接代入求解,判断即可得出结论.
(2010重庆文数)(3)若向量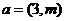 ,
,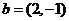 ,
,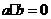 ,则实数
,则实数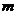 的值为
的值为
(A) (B)
(B)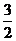
(C)2 (D)6
解析: ,所以
,所以 =6
=6
(2010重庆理数)(2) 已知向量a,b满足 ,则
,则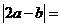
A. 0
B.

 C. 4 D. 8
C. 4 D. 8
解析: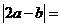
(2010山东文数)(12)定义平面向量之间的一种运算“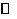 ”如下:对任意的
”如下:对任意的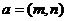 ,
,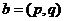 ,令
,令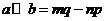 ,下面说法错误的是
,下面说法错误的是
(A)若a与b共线,则
(B)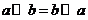
(C)对任意的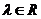 ,有
,有
(D)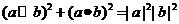
答案:B
(2010四川理数)(5)设点M是线段BC的中点,点A在直线BC外,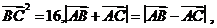 则
则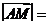
(A)8 (B)4 (C) 2 (D)1
解析:由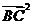 =16,得|BC|=4
=16,得|BC|=4
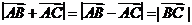 =4
=4
而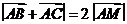
故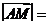 2
2
答案:C
(2010天津文数)(9)如图,在ΔABC中,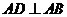 ,
,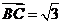
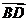 ,
,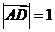 ,则
,则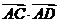 =
=
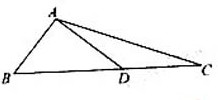 (A)
(A)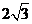 (B)
(B)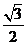 (C)
(C)
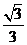 (
( D)
D)
[答案]D
[解析]本题主要考查 平面向量的基本运算与解三角形的基础知识,属于难题。
平面向量的基本运算与解三角形的基础知识,属于难题。
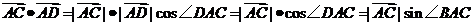

[温馨提示]近几年天津卷中总可以看到平面向量的身影,且均属于中等题或难题,应加强平面向量的基本运算 的
的 训练,尤其是与三角形综合的问题。
训练,尤其是与三角形综合的问题。
(2010广东文数)

(2010福建文数)

(2010全国卷1文数)(11)已知圆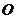 的半径为1,PA、PB为该圆的两条切线
的半径为1,PA、PB为该圆的两条切线 ,A、B为两切点,那么
,A、B为两切点,那么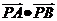 的最小值为
的最小值为
(A) 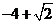 (B)
(B)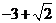 (C)
(C) 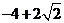 (D)
(D)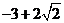
6.(2010湖南文数) 若非零向量a,b满足|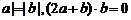 ,则a与b的夹角为
,则a与b的夹角为
A. 300 B. 600 C. 1200  D. 1500
D. 1500
(2010全国卷2理数)(8)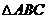 中,点
中,点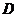 在
在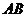 上,
上,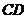 平方
平方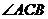 .若
.若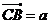 ,
,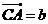 ,
,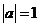 ,
,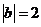 ,则
,则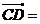
(A)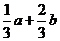 (B)
(B)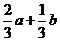 (C)
(C)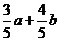 (D)
(D)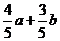
[答案]B
[命题意图]本试题主要考查向量的基本运算,考查角平分线定理.
[解析]因为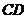 平分
平分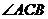 ,由角平分线定理得
,由角平分线定理得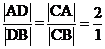 ,所以D为AB的三等分点,且
,所以D为AB的三等分点,且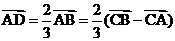 ,所以
,所以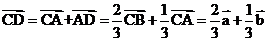 ,故选B.
,故选B.
(2010辽宁文数)(8)平面上 三点不共线,设
三点不共线,设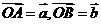 ,则
,则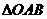 的面积等于 K^S*5U.C#
的面积等于 K^S*5U.C#
(A)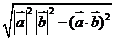 (B)
(B)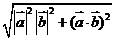
(C)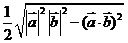 (D)
(D)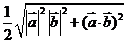
解析:选C.
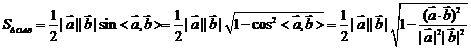
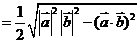
(2010辽宁理数)(8)平面上O,A,B三点不共线,设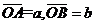 ,则△OAB的面积等于
,则△OAB的面积等于
(A)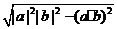 (B)
(B) 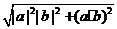
(C) 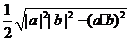
 (D)
(D) 
[答案]C
[命题立意]本题考查了三角形面积的向量表示,考查了向量的内积以及同角三角函数的基本关系。
[解析]三角形的面积S=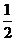 |a||b|sin<a,b>,而
|a||b|sin<a,b>,而
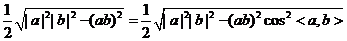

(2010全国卷2文数)(10)△ABC中,点D在边AB上,CD平分∠ACB,若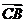 = a ,
= a , 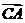 =
b ,
=
b , 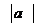 =
1 ,
=
1 ,
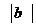 = 2, 则
= 2, 则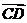 =
=
(A)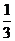 a +
a + 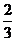 b (B)
b (B)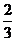 a +
a +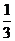 b (C)
b (C)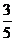 a +
a +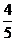 b (D)
b (D)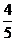 a +
a +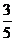 b
b
[解析]B:本题考查了平面向量的基础知识
∵ CD为角平分线,∴ 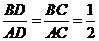 ,∵
,∵
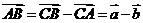 ,∴
,∴
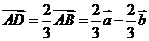 ,∴
,∴
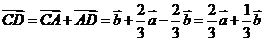
(2010安徽文数)(3)设向量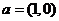 ,
,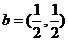 ,则下列结论中正确的是
,则下列结论中正确的是
(A)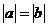 (B)
(B)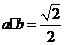
(C)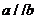 (D)
(D)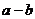 与
与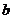 垂直
垂直
5.(浙江卷理10)设函数的集合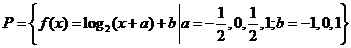 ,
,
平面上点的集合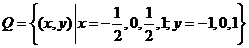 ,则在同一直角坐标系中,
,则在同一直角坐标系中,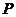 中函数
中函数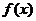 的图象恰好经过
的图象恰好经过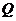 中两个点的函数的个数是
中两个点的函数的个数是
(A)4 (B)6 (C)8 (D)10
解析:当a=0,b=0;a=0,b=1;a=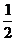 ,b=0; a=
,b=0; a=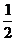 ,b=1;a=1,b=-1;a=1,b=1时满足题意,故答案选B,本题主要考察了函数的概念、定义域、值域、图像和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的考察,属中档题
,b=1;a=1,b=-1;a=1,b=1时满足题意,故答案选B,本题主要考察了函数的概念、定义域、值域、图像和对数函数的相关知识点,对数学素养有较高要求,体现了对能力的考察,属中档题
4.(山东卷理12文12)定义平面向量之间的一种运算“⊙”如下,对任意的a=(m,u),b=(p,q),另a⊙b=mq-np,下面的说法错误的是
(A)若a与b共线,则a⊙b=0
(B)a⊙b=b⊙a
(C)对任意的λ∈R,有(λa)⊙b=λ(a⊙b)
(D)(a⊙b)2+(a·b)2=|a|2 |b|2
[答案]B
[解析]若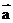 与
与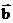 共线,则有
共线,则有 ,故A正确;因为
,故A正确;因为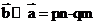 ,而
,而
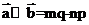 ,所以有
,所以有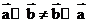 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
3.(湖北卷理10文10)记实数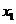 ,
, ,……
,……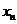 中的最大数为max
中的最大数为max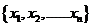 ,最小数为min
,最小数为min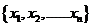 。已知ABC的三边长位a,b,c(
。已知ABC的三边长位a,b,c(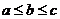 ),定义它的亲倾斜度为
),定义它的亲倾斜度为
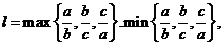 则“
则“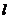 =1”是“
=1”是“ ABC为等边三角形”的
ABC为等边三角形”的
A.必要而不充分的条件 B.充分而不必要的条件
C.充要条件 D.既不充分也不必要条件
[答案]A
[解析]若△ABC为等边三角形时,即a=b=c,则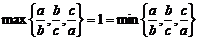 则l=1;若△ABC为等腰三角形,如a=2,b=2,c=3时,
则l=1;若△ABC为等腰三角形,如a=2,b=2,c=3时,
则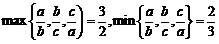 ,此时l=1仍成立但△ABC不为等边三角形,所以A正确.
,此时l=1仍成立但△ABC不为等边三角形,所以A正确.
2.(广东卷文10)在集合{a,b,c,d}上定义两种运算 和
和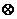 如下:
如下:

那么d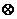
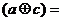
A.a B.b C.c D.d
解:由上表可知: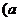 +
+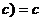 ,故
,故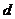 *
*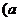 +
+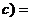
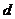 *
*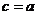 ,选A。
,选A。
1.(福建卷理10)对于具有相同定义域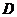 的函数
的函数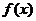 和
和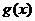 ,若存在函数
,若存在函数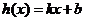 (
(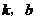 为常数),对任给的正数
为常数),对任给的正数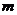 ,存在相应的
,存在相应的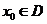 ,使得当
,使得当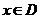 且
且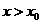 时,总有
时,总有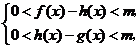 则称直线
则称直线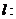
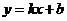 为曲线
为曲线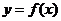 与
与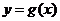 的“分渐近线”。给出定义域均为D=
的“分渐近线”。给出定义域均为D= 的四组函数如下:
的四组函数如下:
①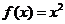 ,
,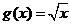 ;②
;②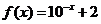 ,
,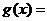
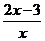 ;
;
③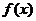
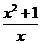 ,
,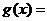
 ;④
;④ ,
,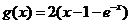 。
。
其中,曲线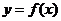 与
与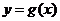 存在“分渐近线”的是
存在“分渐近线”的是
A.①④ B.②③ C.②④ D.③④
[答案]C
[解析]要透过现象看本质,存在分渐近线的充要条件是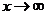 时,
时,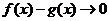 。对于1,当
。对于1,当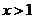 时便不符合,所以1不存在;对于2,肯定存在分渐近线,因为当时,
时便不符合,所以1不存在;对于2,肯定存在分渐近线,因为当时,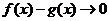 ;对于3,
;对于3, ,设
,设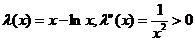 且
且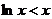 ,所以当
,所以当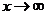 时
时 越来愈大,从而
越来愈大,从而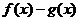 会越来越小,不会趋近于0,所以不存在分渐近线;4当
会越来越小,不会趋近于0,所以不存在分渐近线;4当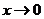 时,
时,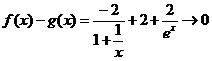 ,因此存在分渐近线。故,存在分渐近线的是24选C
,因此存在分渐近线。故,存在分渐近线的是24选C
[命题意图]本题从大学数列极限定义的角度出发,仿造构造了分渐近线函数,目的是考查学生分析问题、解决问题的能力,考生需要抓住本质:存在分渐近线的充要条件是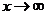 时,
时,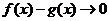 进行做答,是一道好题,思维灵活。
进行做答,是一道好题,思维灵活。
21.(2010湖南文数)(本小题满分13分)
已知函数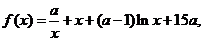 其中a<0,且a≠-1.
其中a<0,且a≠-1.
(Ⅰ)讨论函数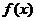 的单调性;
的单调性;
(Ⅱ)设函数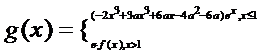 (e是自然数的底数)。是否存在a,使
(e是自然数的底数)。是否存在a,使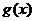 在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。



(2010浙江理数) (22)(本题满分14分)已知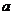 是给定的实常数,设函数
是给定的实常数,设函数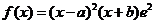 ,
,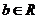 ,
,
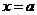 是
是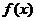 的一个极大值点.
的一个极大值点.
(Ⅰ)求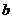 的取值范围;
的取值范围;
(Ⅱ)设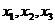 是
是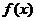 的3个极值点,问是否存在实数
的3个极值点,问是否存在实数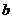 ,可找到
,可找到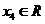 ,使得
,使得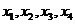 的某种排列
的某种排列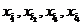 (其中
(其中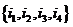 =
=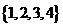 )依次成等差数列?若存在,求所有的
)依次成等差数列?若存在,求所有的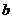 及相应的
及相应的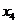 ;若不存在,说明理由.
;若不存在,说明理由.
解析:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识。
(Ⅰ)解:f’(x)=ex(x-a)
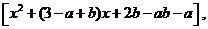
令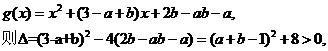
于是,假设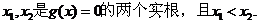
(1) 当x1=a 或x2=a时,则x=a不是f(x)的极值点,此时不合题意。
(2) 当x1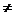 a且x2
a且x2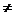 a时,由于x=a是f(x)的极大值点,故x1<a<x2.
a时,由于x=a是f(x)的极大值点,故x1<a<x2.
即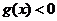
即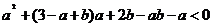
所以b<-a
所以b的取值范围是(-∞,-a)
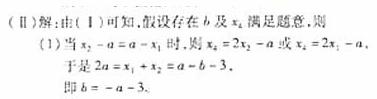
此时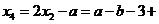
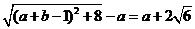
或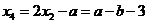
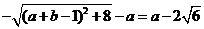
(2)当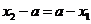 时,则
时,则 或
或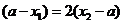
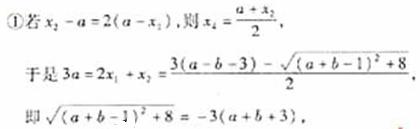
于是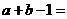
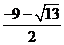
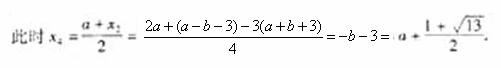
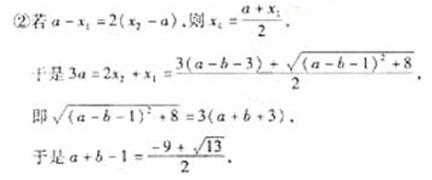
此时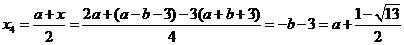
综上所述,存在b满足题意,
当b=-a-3时,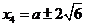
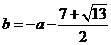 时,
时,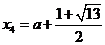
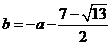 时,
时,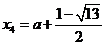
(2010全国卷2理数)(22)(本小题满分12分)
设函数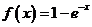 .
.
(Ⅰ)证明:当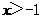 时,
时,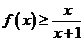 ;
;
(Ⅱ)设当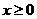 时,
时,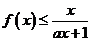 ,求a的取值范围.
,求a的取值范围.
[命题意图]本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力.
22.(2010上海文数)(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分。
若实数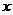 、
、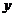 、
、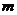 满足
满足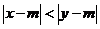 ,则称
,则称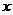 比
比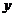 接近
接近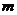 .
.
(1)若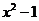 比3接近0,求
比3接近0,求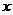 的取值范围;
的取值范围;
(2)对任意两个不相等的正数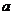 、
、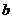 ,证明:
,证明: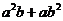 比
比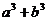 接近
接近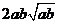 ;
;
(3)已知函数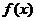 的定义域
的定义域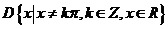 .任取
.任取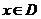 ,
,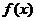 等于
等于 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数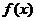 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
解析:(1) xÎ(-2,2);
(2) 对任意两个不相等的正数a、b,有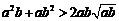 ,
,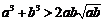 ,
因为
,
因为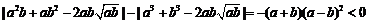 ,
所以
,
所以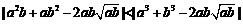 ,即a2b+ab2比a3+b3接近
,即a2b+ab2比a3+b3接近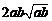 ;
(3)
;
(3) 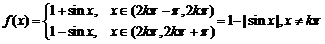 ,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间
,kÎZ,
f(x)是偶函数,f(x)是周期函数,最小正周期T=p,函数f(x)的最小值为0,
函数f(x)在区间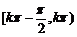 单调递增,在区间
单调递增,在区间 单调递减,kÎZ.
单调递减,kÎZ.
6. (2010江苏卷)14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是____▲____。
,则S的最小值是____▲____。
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小 正三角形的边长为
正三角形的边长为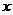 ,
, 则:
则: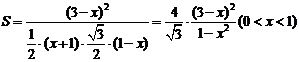
(方法一)利用导数求函数最小值。
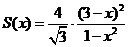 ,
,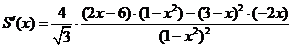
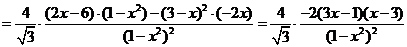
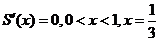 ,
,
当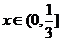 时,
时,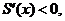 递减;当
递减;当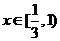 时,
时,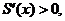 递增;
递增;
故当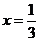 时,S的最小值是
时,S的最小值是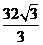 。
。
(方法二)利用函数的方法求最小值。
令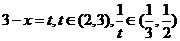 ,则:
,则: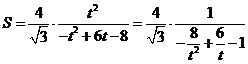
故当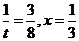 时,S的最小值是
时,S的最小值是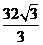 。
。
2010年高考数学试题分类汇编--函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com