
8.(2010江西理数)直线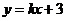 与圆
与圆 相交于M,N两点,若
相交于M,N两点,若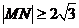 ,则k的取值范围是
,则k的取值范围是
A. 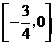 B.
B.
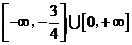 C.
C. 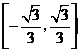 D.
D.
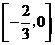
 [答案]A
[答案]A
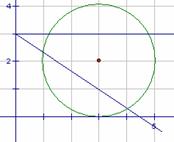
[解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
解法1:圆心的坐标为(3.,2),且圆与y轴相切.当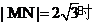 ,由点到直线距离公式,解得
,由点到直线距离公式,解得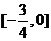 ;
;
解法2:数形结合,如图由垂径定理得夹在两直线之间即可, 不取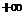 ,排除B,考虑区间不对称,排除C,利用斜率估值,选A
,排除B,考虑区间不对称,排除C,利用斜率估值,选A
(2010安徽文数)(4)过点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 (D)x+2y-1=0
6.(2010湖北理数)将参加夏令营的600名学生编号为:001,002,……600,采用系统抽样方 法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数一次为
法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到300在第Ⅰ营区,从301到495住在第Ⅱ营区,从496到600在第Ⅲ营区,三个营区被抽中的人数一次为
A.26, 16, 8, B.25,17,8
C.25,16,9 D.24,17,9

1. (2010湖北理数)4.投掷一枚均匀硬币和一枚均匀骰子各一次,记“硬币正面向上”为事件A,“骰子向上的点数是3”为事件B,则事件A,B中至少有一件发生的概率是
A 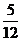 B
B 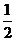 C
C 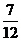
 D
D 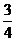

7.B.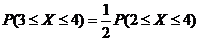 =0.3413,
=0.3413,
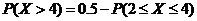 =0.5-
=0.5- 0.3413=0.1587.
0.3413=0.1587.
(2010四川文数)(4)一个单位有职工800人,期中具有高级职称的160人, 具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是
具有中级职称的320人,具有初级职称的200人,其余人员120人.为了解职工收入情况,决定采用分层抽样的方法,从中抽取容量为40的样本.则从上述各层中依次抽取的人数分别是
(A)12,24,15,9 (B)9,12,12,7 (C)8,15,12,5 (D)8,16,10,6
解析:因为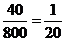
故各层中依次抽取的人数分别是 ,
, ,
,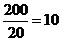 ,
,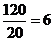
答案:D
(2010山东理数)(8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
(A)36种 (B)42种 (C)48种 (D)54种
[答案]B

(2010山东理数)

(2010山东理数)

7.(2010广东理数)已知随机变量X服从正态分布N(3.1),且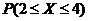 =0.6826,则p(X>4)=( )
=0.6826,则p(X>4)=( )
A、0.1588 B、0.1587 C、0.1586 D0.1585
8.C.每次闪烁时间5秒,共5×120=600s,每两次闪烁之间 的间隔为5s,共5×(120-1)=595s.总共就有600+595=1195s.
的间隔为5s,共5×(120-1)=595s.总共就有600+595=1195s.
8.(2010广东理数)为了迎接2010年广州亚运会,某大楼安装5个彩灯,它们闪亮的顺序不固定,每个彩灯彩灯闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯所闪亮的颜色各不相同.记这5个彩灯有序地闪亮一次为一个闪烁,在每个闪烁中,每秒钟有且仅有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5秒。如果要实现所有不同的闪烁,那么需要的时间至少是( )
A、 1205秒 B.1200秒 C.1195秒  D.1190秒
D.1190秒
10.C
[解析]正方形四个顶点可以确定6条直线,甲乙各自任选一条共有36个基本事件。两条直线相互垂直的情况有5种(4组邻边和对角线)包括10个基本事件,所以概率等于.
[方法技巧]对于几何中的概率问题,关键是正确作出几何图形,分类得出基本事件数,然后得所求事件保护的基本事件数,进而利用概率公式求概率.
(2010重庆文数)(5)某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为
(A)7 (B)15 (C)25 (D)35
解析:青年职工、中年职工、老年 职工三层之比为7:5:3,所以样本容量为
职工三层之比为7:5:3,所以样本容量为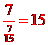
(2010山东文数)(6)在某项体育比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)92 , 2
 (B) 92 ,
2.8
(B) 92 ,
2.8
(C) 93 , 2 (D) 93 , 2.8
答案:B
(2010北京文数)⑶从{1,2,3,4,5}中随机选取一个 数为a,从{1,2,3}中随机选取一个数为b,则b>a的
数为a,从{1,2,3}中随机选取一个数为b,则b>a的 概率是
概率是
(A)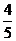 (B)
(B)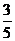 (C)
(C)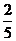 (D)
(D)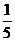
答案:D
11.(2010江西理数)一位国王的铸币大臣在每箱1 00枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测。方法一:在10箱子中各任意抽查一枚;方法二:在5箱中各任意抽查两枚。国王用方法一、二能发现至少一枚劣币的概率分别为
00枚的硬币中各掺入了一枚劣币,国王怀疑大臣作弊,他用两种方法来检测。方法一:在10箱子中各任意抽查一枚;方法二:在5箱中各任意抽查两枚。国王用方法一、二能发现至少一枚劣币的概率分别为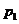 和
和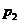 ,则
,则
A. 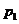 =
=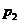 B.
B. 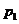 <
<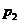
 C.
C. 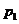 >
>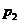 D。以上三种情况都有可能
D。以上三种情况都有可能
[答案]B
[解析]考查不放回的抽球、重点考查二项分布的概率。本题是北师大版新课标的课 堂作业,作为旧大纲的最后一年高考,本题给出一个强烈的导向信号。方法一:每箱的选中的概率为
堂作业,作为旧大纲的最后一年高考,本题给出一个强烈的导向信号。方法一:每箱的选中的概率为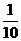
,总概率为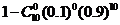 ;同理,方法二:每箱的选中的概率为
;同理,方法二:每箱的选中的概率为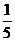 ,总事件的概率为
,总事件的概率为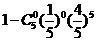 ,作差得
,作差得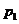 <
<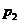 。
。
(2010安徽文数)(10)甲从正方形四个顶点中任意选择两个顶点连成直线,乙从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是
(A)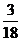 (A)
(A)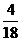 (A)
(A)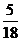 (A)
(A)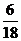
3. (湖南卷文4)极坐标
(湖南卷文4)极坐标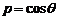 和参数方程
和参数方程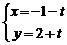 (t为参数)所表示的图形分别是
(t为参数)所表示的图形分别是
A. 直线、直线 B. 直线、圆 C. 圆、圆 D. 圆、直线
 D
D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com